Wie prüfe ich mit drei Seitenlängen, ob ein Dreieck rechtwinklig ist?

Du prüfst ein Dreieck mit drei Seitenlängen auf Rechtwinkligkeit, indem du die längste Seite als mögliche Hypotenuse nimmst und testest, ob gilt. Zum Beispiel ist bei 5, 12 und 13 die 13 die längste Seite und , also rechtwinklig.

Welche Fehler passieren oft beim Satz des Pythagoras?

Häufige Fehler beim Satz des Pythagoras sind: die falsche Seite als Hypotenuse zu wählen (Hypotenuse ist immer die längste Seite), Vorzeichenfehler beim Umformen (, nicht ) und das Vergessen der Wurzel am Ende. Beispiel: Aus folgt , nicht .

Wann darf ich den Satz des Pythagoras nicht benutzen?

Den Satz des Pythagoras darfst du nicht benutzen, wenn das Dreieck nicht rechtwinklig ist, also keinen 90°-Winkel hat. Außerdem passt er nicht für beliebige Vierecke oder schiefe Dreiecke ohne rechten Winkel. Beispiel: In einem Dreieck mit Winkeln 60°, 60°, 60° führt zu falschen Ergebnissen.

Wie entscheide ich, ob ich Pythagoras oder den Kathetensatz nutze?

Du nutzt Pythagoras, wenn du in einem rechtwinkligen Dreieck Katheten , und Hypotenuse direkt verknüpfst. Den Kathetensatz nutzt du, wenn die Hypotenuse durch die Höhe in Abschnitte und geteilt ist und du mit oder rechnen kannst.

Wie berechne ich die Höhe auf die Hypotenuse im rechtwinkligen Dreieck?

Die Höhe auf die Hypotenuse berechnest du im rechtwinkligen Dreieck entweder mit dem Höhensatz (wenn die Hypotenusenabschnitte und bekannt sind) oder über die Flächenformel , also .

Video

Quiz

Hier geht's zum Video „Dreieck“

Hier geht's zum Video „Umfang Dreieck“

Hier geht's zum Video „Flächeninhalt Dreieck“

Hier geht's zum Video „Rechteck“

Hier geht's zum Video „Satz des Pythagoras“

Hier geht's zum Video „Äquivalenzumformung“

Hier geht's zum Video „Höhensatz“

Hier geht's zum Video „Kathetensatz“

Hier geht's zum Video „Höhen- und Kathetensatz“

Rechtwinkliges Dreieck

Wichtige Inhalte in diesem Video

Rechtwinkliges Dreieck einfach erklärt

(00:14)

Umfang und Flächeninhalt rechtwinkliges Dreieck

(01:18)

Rechtwinkliges Dreieck berechnen

(02:52)

Was ist ein rechtwinkliges Dreieck und wie kannst du es berechnen? Hier und in unserem Video erfährst du alles, was du wissen musst!

Inhaltsübersicht

Rechtwinkliges Dreieck einfach erklärt

im Videozur Stelle im Video springen

(00:14)

Ein rechtwinkliges Dreieck erkennst du an seinem 90°-Winkel (rechter Winkel). Die Seiten neben dem rechten Winkel nennst du Katheten a und b. Die Seite, die gegenüber vom 90°-Winkel liegt, ist die Hypotenuse c. Sie ist immer die längste Seite im Dreieck.

Rechtwinkliges Dreieck, Rechtwinkliges Dreieck berechnen, Flächeninhalt Rechtwinkliges Dreieck, Rechtwinkliges Dreieck Formeln, Formel Rechtwinkliges Dreieck, Rechtwinklige Dreiecke, Winkel Rechtwinkliges Dreieck, Dreieck rechtwinklig, Höhe Rechtwinkliges Dreieck, Dreieck beschriften, Rechtwinkliges Dreieck Winkel, Winkel im rechtwinkligen Dreieck, Rechter Winkel Dreieck, Dreieck mit rechtem Winkel, Rechtwinkliges Dreieck Eigenschaften, Dreieck rechter Winkel, Umfang rechtwinkliges Dreieck — Rechtwinkliges Dreieck

Du kannst das rechtwinklige Dreieck beschriften: Für die Eckpunkte benutzt du große Buchstaben in alphabetischer Reihenfolge (A, B, C). Du beschriftest die Ecken dabei gegen den Uhrzeigersinn. Die Seiten kannst du genauso mit kleinen Buchstaben beschriften (a, b, c).

Die Katheten a und b haben besondere Namen. Schau sie dir am Winkel α an: Die Seite, die gegenüber vom Winkel α liegt, ist seine Gegenkathete von α (hier: a). Die Seite, die an dem Winkel α liegt, ist seine Ankathete von α (hier: b).

Katheten und Hypotenuse

Die längste Seite ist immer die Hypotenuse c. Die Seite gegenüber vom betrachteten Winkel heißt Gegenkathete und die Seite an dem betrachteten Winkel nennst du Ankathete!

Umfang und Flächeninhalt rechtwinkliges Dreieck

im Videozur Stelle im Video springen

(01:18)

Den Umfang U eines rechtwinkligen Dreiecks bekommst du, indem du die Seitenlängen a, b und c zusammenrechnest. Die Formel für den Umfang ist also:

U = a + b + c

Beispiel: Berechne den Umfang des Dreiecks mit den Seitenlängen a = 20 cm, b = 21 cm und c = 29 cm.

U = a + b + c

U = 20 cm + 21 cm + 29 cm

U = 70 cm

Super!

Den Flächeninhalt A eines rechtwinkligen Dreiecks berechnest du mit der Formel

A = ½ · a · b

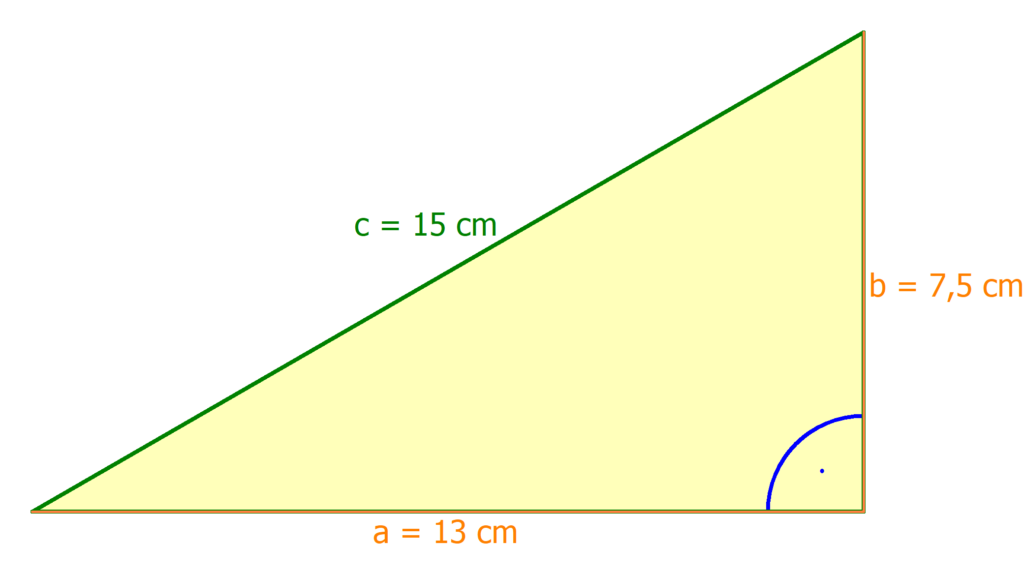
Beispiel: Berechne den Flächeninhalt eines rechtwinkligen Dreiecks mit den Seitenlängen a = 13 cm, b = 7,5 cm und c = 15 cm.

Um den Flächeninhalt zu berechnen, setzt du einfach die Werte in die Formel ein:

A = ½ · a · b

A = ½ · 13 cm · 7,5 cm

A = 48,75 cm²

Herleitung Formel Flächeninhalt

Die Formel A = ½ · a · b kannst du dir übrigens ganz einfach herleiten: Spiegelst du das Dreieck entlang seiner Hypotenuse, entsteht ein Rechteck. Seine Fläche kannst du mit der Formel A = a · b berechnen. Um dann den Flächeninhalt des rechtwinkligen Dreiecks zu bekommen, teilst du das Ergebnis durch 2 oder rechnest mal ½!

Doch du kannst nicht nur den Flächeninhalt berechnen!

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Rechtwinkliges Dreieck berechnen

im Videozur Stelle im Video springen

(02:52)

Es gibt verschiedene Formeln, die dir helfen, ein rechtwinkliges Dreieck zu berechnen. Eine der wichtigsten Formeln für ein rechtwinkliges Dreieck ist der Satz des Pythagoras!

Satz des Pythagoras

Der Satz des Pythagoras hilft dir, die einzelnen Seiten des Dreiecks zu berechnen. Er lautet:

c² = a² + b²

Durch Umformen , erhältst du für die Seitenlängen die Formeln:

c = $\sqrt{a^2 +b^2}$
a = $\sqrt{c^2 - b^2}$
b = $\sqrt{c^2 - a^2}$

Beispiel: Ein Dreieck hat die Längen c = 10 cm und a = 6 cm. Berechne die fehlende Länge b.

Da du die Länge b suchst, benutzt du die Formel

b = $\sqrt{c^2 - a^2}$

Setze deine Werte ein und rechne das Ergebnis aus.

b = $\sqrt{(10 cm)^2 - (6 cm)^2}$

b = $\sqrt{100 cm^2 - 36 cm^2}$

b = 8 cm

Kathetensatz und Höhensatz

Durch die Höhe h im rechtwinkligen Dreieck kann die Hypotenuse c auch in die Seiten p und q geteilt werden.

Daraus ergeben sich neue Formeln für rechtwinklige Dreiecke, mit denen du die fehlenden Seiten berechnen kannst.

Höhensatz

h² = p · q

Kathetensatz

a² = p · c
b² = q · c

Wenn du dir ein paar Beispiele zum Höhen- und Kathetensatz anschauen möchtest, bist du bei diesem Video genau richtig!

Rechtwinkliges Dreieck — häufigste Fragen

(ausklappen)

Wie prüfe ich mit drei Seitenlängen, ob ein Dreieck rechtwinklig ist?

Du prüfst ein Dreieck mit drei Seitenlängen auf Rechtwinkligkeit, indem du die längste Seite als mögliche Hypotenuse nimmst und testest, ob gilt. Zum Beispiel ist bei 5, 12 und 13 die 13 die längste Seite und , also rechtwinklig.
Welche Fehler passieren oft beim Satz des Pythagoras?

Häufige Fehler beim Satz des Pythagoras sind: die falsche Seite als Hypotenuse zu wählen (Hypotenuse ist immer die längste Seite), Vorzeichenfehler beim Umformen (, nicht ) und das Vergessen der Wurzel am Ende. Beispiel: Aus folgt , nicht .
Wann darf ich den Satz des Pythagoras nicht benutzen?

Den Satz des Pythagoras darfst du nicht benutzen, wenn das Dreieck nicht rechtwinklig ist, also keinen 90°-Winkel hat. Außerdem passt er nicht für beliebige Vierecke oder schiefe Dreiecke ohne rechten Winkel. Beispiel: In einem Dreieck mit Winkeln 60°, 60°, 60° führt zu falschen Ergebnissen.
Wie entscheide ich, ob ich Pythagoras oder den Kathetensatz nutze?

Du nutzt Pythagoras, wenn du in einem rechtwinkligen Dreieck Katheten , und Hypotenuse direkt verknüpfst. Den Kathetensatz nutzt du, wenn die Hypotenuse durch die Höhe in Abschnitte und geteilt ist und du mit $a^2 = p \cdot c$ oder $b^2 = q \cdot c$ rechnen kannst.
Wie berechne ich die Höhe auf die Hypotenuse im rechtwinkligen Dreieck?

Die Höhe auf die Hypotenuse berechnest du im rechtwinkligen Dreieck entweder mit dem Höhensatz $h^2 = p \cdot q$ (wenn die Hypotenusenabschnitte und bekannt sind) oder über die Flächenformel $A = \frac{1}{2}ab = \frac{1}{2}ch$ , also $h = \frac{a \cdot b}{c}$ .

Gleichschenkliges Dreieck

Das rechtwinklige Dreieck ist nicht die einzige Dreiecksart . Was es zum Beispiel mit dem gleichschenkligen Dreieck auf sich hat und wie du es berechnest, zeigen wir dir hier!