Wie erkenne ich in einer Aufgabe, ob wirklich eine Kugel gemeint ist?

Eine Kugel ist gemeint, wenn ein vollständig runder Körper ohne Kanten beschrieben wird und alle Oberflächenpunkte gleich weit vom Mittelpunkt entfernt sind. Typische Hinweise sind Angaben wie Radius, Durchmesser oder „kugelförmig“. Ist beispielsweise der Wert für den Durchmesser einer Kugel gegeben, dann passt die Kugelformel.

Welche Fehler passieren oft, wenn ich den Radius aus dem Durchmesser berechne?

Häufige Fehler sind, den Radius fälschlich gleich dem Durchmesser zu setzen oder beim Halbieren die Einheit zu vergessen. Richtig ist immer . Beispiel: Bei ist .

Wie rechne ich das Kugelvolumen um, wenn Liter gefragt sind?

Liter sind eine Volumeneinheit, daher muss das Ergebnis nur in die passende Einheit umgerechnet werden: . Beispiel: entsprechen , weil .

Wie berechne ich das Volumen einer halben Kugel?

Das Volumen einer halben Kugel (Halbkugel) ist die Hälfte des Kugelvolumens, also . Das gilt, wenn wirklich nur die „halbe Kugel“ ohne zusätzlichen Zylinder gemeint ist.

Warum wächst das Kugelvolumen so stark, wenn der Radius größer wird?

Das Kugelvolumen wächst so stark, weil es proportional zu ist: . Wenn der Radius größer wird, wird der Faktor dreimal „mitvergrößert“ (in drei Raumrichtungen). Beispiel: Verdoppelt sich , wird achtmal so groß, weil .

Video

Quiz

Hier geht's zum Video „Oberfläche Kugel“

Volumen Kugel

Wichtige Inhalte in diesem Video

Kugelvolumen berechnen

(00:45)

Anwendungsbeispiel

(01:34)

Du willst wissen, was eine Kugel ist und wie du das Kugel Volumen berechnen kannst? Hier und in unserem Video , zeigen wir dir, wie’s geht!

Inhaltsübersicht

Volumen Kugel berechnen einfach erklärt

Eine Kugel ist ein komplett runder, geometrischer Körper ohne Ecken und Kanten. Ein Globus, ein Fußball oder eine Eiskugel — all das sind Kugeln, die dir im Alltag begegnen.

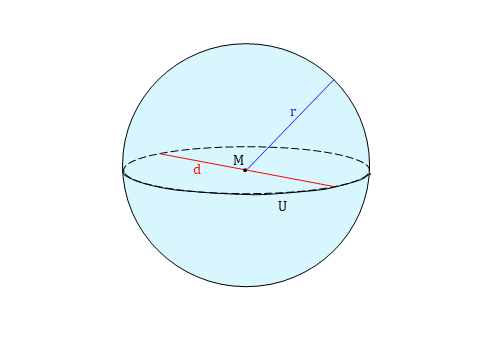
Eine Kugel hat einen Mittelpunkt M. Alle Punkte auf der Kugeloberfläche sind gleich weit von ihm entfernt. Diesen Abstand beschreibst du mit dem Radius r. Der Durchmesser d gibt dagegen den Abstand von zwei gegenüberliegenden Punkten an. Er ist doppelt so lang wie der Radius r und geht durch den Mittelpunkt M.

Kugel Volumen

Das Volumen einer Kugel berechnest du mit der Formel

V = 4/3 · π · r³

Beispiel: Eine Kugel mit dem Radius 2 cm hat ein Volumen von V = 4/3 · π · (2 cm)³ ≈ 33,5 cm³.

Tipp: Die Kreiszahl (Pi) π ≈ 3,1415… ist in deinem Taschenrechner eingespeichert. Du kannst aber auch den gerundeten Wert π ≈ 3,14 verwenden.

Kugelvolumen berechnen

im Videozur Stelle im Video springen

(00:45)

Das Volumen der Kugel mit der Formel zu bestimmen, geht in wenigen Schritten. Dafür muss nur der Radius r gegeben sein.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Beispiel 1

Berechnen wir zuerst das Volumen einer Kugel mit dem Radius r = 5 cm.

Kugelvolumen, Volumen Kugel — Kugelvolumen: Beispiel 1

Kugel Formel aufstellen: Am besten schreibst du dir dafür erstmal die Formel auf.

$V = \frac{4}{3} \cdot \pi \cdot \textcolor{blue}{r}^3$

Radius einsetzen: Dann setzt du den gegebenen Wert für r ein.

$V = \frac{4}{3} \cdot \pi \cdot (\textcolor{blue}{5\text{cm}})^3$

Ergebnis berechnen: Zum Schluss musst du nur noch alle Werte zusammenrechnen.

$V \approx 523,6\text{cm}^3$

Hinweis: Das Kugelvolumen wird immer in einer Maßeinheit für das Volumen angegeben, so wie hier mit cm³.

Beispiel 2

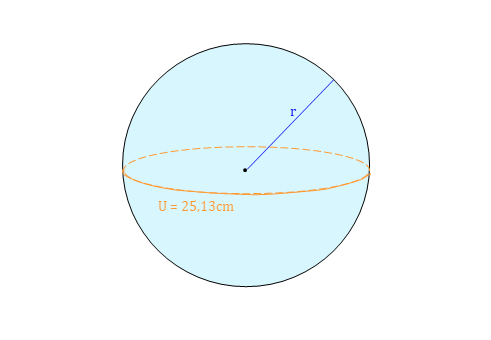
Um das nächste Volumen der Kugel berechnen zu können, musst du zuerst den Radius bestimmen. Gegeben ist für die Kugel nämlich nur der Umfang U = 25,13 cm.

Volumen Kugel, Umfang Kugel, Kugelvolumen, Kugel Volumen — Volumen Kugel aus Umfang

Umfangsformel aufstellen: Du beginnst erstmal mit der Formel für den Umfang. Das ist die gleiche wie beim Umfang vom Kreis .

$U=2 \cdot r \cdot \pi$

Nach r auflösen: Stell die Formel so um, dass du damit den Radius r berechnen kannst.

$\begin{align*} 2 \cdot r \cdot \pi &= U && |: 2 \\ r \cdot \pi &= \frac{U}{2} && |: \pi \\ r &= \frac{U}{2 \cdot \pi} \end{align*}$

Radius berechnen: Jetzt kannst du aus dem Umfang den Radius bestimmen.

$r = \frac{25,13\text{cm}}{2 \cdot \pi} \approx 4\text{cm}$

Formel für Kugelvolumen aufstellen: Aus diesem Wert kannst du nun ganz normal das Kugelvolumen berechnen.

$V = \frac{4}{3} \cdot r^3 \cdot \pi$

Radius einsetzen:

$V = \rac{4}{3} \cdot \pi \cdot (4 \text{cm})^3$

Ergebnis berechnen:

$V \approx 268,08\text{cm}^3$

Anwendungsbeispiel

im Videozur Stelle im Video springen

(01:34)

Für ein Fest sollen große Wasserlaufbälle aufgepumpt werden. Jeder dieser Bälle hat einen Durchmesser von 2 Metern. Wie viel Luft brauchst du, um einen Ball vollständig aufzupumpen?

Dieses Anwendungsbeispiel kannst du mit dem Kugelvolumen lösen. Wieder brauchst du die Formel für das Volumen der Kugel zur Berechnung.

Kugelvolumen Formel aufstellen:

$V=\frac{4}{3} \cdot \pi \cdot r^3$

Radius berechnen: Weil in der Angabe nur der Durchmesser d = 2 m genannt ist, musst du zuerst den Radius berechnen.

$d=2 \cdot r$

$r=\frac{d}{2}$

$r=\frac{2\text{m}}{2} = 1\text{m}$

Radius einsetzen:

$V=\frac{4}{3} \cdot \pi \cdot (1\text{m})^3$

Ergebnis berechnen:

$V \approx 4,19\text{m}^3$

In jeden großen Wasserlaufball passen ungefähr 4,19m³ Luft.

Kugel Volumen Formel umstellen

Wenn du das Volumen einer Kugel gegeben hast, kannst du daraus den Radius berechnen. In unserem Beispiel hast du ein Kugelvolumen von V = 4188,8 cm³ gegeben. Berechne nun den Radius!

Kugel Volumen Formel aufstellen:

$V = \frac{4}{3} \cdot \pi \cdot r^3$

Nach r auflösen:

$\begin{align*} \frac{4}{3} \cdot \pi \cdot r^3 &= V && | : \pi \\ \frac{4}{3} \cdot r^3 &= \frac{V}{\pi} && | \cdot \frac{3}{4} \\ r^3 &= \frac{3 \cdot V}{4 \cdot \pi} && | \sqrt[3]{...} \\ r &= \sqrt[3]{\frac{3 \cdot V}{4 \cdot \pi}} \end{align*}$

Angabe einsetzen:

$r = \sqrt[3]{\frac{3 \cdot 4188,8\text{cm}^3}{4 \cdot \pi}}$

Ergebnis berechnen:

$r = \sqrt[3]{1000\text{cm}^3} = 10\text{cm}$

Wenn du dir das Formel umstellen nochmal anschauen willst, haben wir hier ein extra Video für dich vorbereitet.

Volumen Kugel — häufigste Fragen

(ausklappen)

Wie erkenne ich in einer Aufgabe, ob wirklich eine Kugel gemeint ist?

Eine Kugel ist gemeint, wenn ein vollständig runder Körper ohne Kanten beschrieben wird und alle Oberflächenpunkte gleich weit vom Mittelpunkt entfernt sind. Typische Hinweise sind Angaben wie Radius, Durchmesser oder „kugelförmig“. Ist beispielsweise der Wert für den Durchmesser einer Kugel gegeben, dann passt die Kugelformel.
Welche Fehler passieren oft, wenn ich den Radius aus dem Durchmesser berechne?

Häufige Fehler sind, den Radius fälschlich gleich dem Durchmesser zu setzen oder beim Halbieren die Einheit zu vergessen. Richtig ist immer $r=\frac{d}{2}$ . Beispiel: Bei $d=12\,\text{cm}$ ist $r=6\,\text{cm}$ .
Wie rechne ich das Kugelvolumen um, wenn Liter gefragt sind?

Liter sind eine Volumeneinheit, daher muss das Ergebnis nur in die passende Einheit umgerechnet werden: $1\,\text{l}=1\,\text{dm}^3=1000\,\text{cm}^3$ . Beispiel: $2500\,\text{cm}^3$ entsprechen $2{,}5\,\text{l}$ , weil .
Wie berechne ich das Volumen einer halben Kugel?

Das Volumen einer halben Kugel (Halbkugel) ist die Hälfte des Kugelvolumens, also $V=\frac{1}{2}\cdot\frac{4}{3}\pi r^3=\frac{2}{3}\pi r^3$ . Das gilt, wenn wirklich nur die „halbe Kugel“ ohne zusätzlichen Zylinder gemeint ist.
Warum wächst das Kugelvolumen so stark, wenn der Radius größer wird?

Das Kugelvolumen wächst so stark, weil es proportional zu ist: $V=\frac{4}{3}\pi r^3$ . Wenn der Radius größer wird, wird der Faktor dreimal „mitvergrößert“ (in drei Raumrichtungen). Beispiel: Verdoppelt sich , wird achtmal so groß, weil .

Oberfläche Kugel

Jetzt weißt du, wie du das Volumen einer Kugel berechnen kannst! Außerdem kannst du bei einer Kugel noch den Umfang U = 2 · π · r berechnen.

Auch die Formeln O = 4 · π · r² oder O = π · d² für die Oberfläche einer Kugel solltest du kennen. In unserem extra Video zur Kugeloberfläche zeigen wir dir viele Beispiele dazu.