Video

Quiz

Hier geht's zum Video „Normalenvektor“

Hier geht's zum Video „Kreuzprodukt / Vektorprodukt“

Hier geht's zum Video „Koordinatenform in Parameterform“

Parameterform in Koordinatenform

Wichtige Inhalte in diesem Video

Parameterform in Koordinatenform einfach erklärt

Parameterform in Koordinatenform: Aufgaben

In diesem Artikel und unserem Video lernst du, wie du eine Ebene von der Parameterform in die Koordinatenform in der Geometrie umwandelst.

Inhaltsübersicht

Parameterform in Koordinatenform einfach erklärt

im Videozur Stelle im Video springen

Du willst die Ebene E von der Parameterform in die Koordinatenform umwandeln:

$\begin{align*}\text{E:}&\overrightarrow{X}=\textcolor{olive}{\left(\begin{array}{c}1\\3\\4\end{array}\right)}+\lambda\textcolor{blue}{\left(\begin{array}{c}2\\5\\6\end{array}\right)}+\mu\textcolor{blue}{\left(\begin{array}{c}3\\0\\7\end{array}\right)}\end{align*}$

1.Schritt: Bilde den Normalenvektor durch das Kreuzprodukt

Zuerst musst du den Normalenvektor berechnen. Das machst du, indem du das Kreuzprodukt der beiden Spannvektoren bestimmst.

$\textcolor{blue}{\left(\begin{array}{c}2\\5\\6\end{array}\right)}\times\textcolor{blue}{\left(\begin{array}{c}3\\0\\7\end{array}\right)}=\left(\begin{array}{c}5\cdot7-6\cdot0\\6\cdot3-2\cdot7\\2\cdot0-5\cdot3\end{array}\right)\)=\textcolor{red}{\left(\begin{array}{c}35\\4\\-15\end{array}\right)}$

2.Schritt: Stelle einen ersten Ansatz deiner Koordinatenform auf

Mithilfe des Normalenvektors kannst du deine Ebenengleichung in eine neue Form bringen:

$\begin{align*}\text{E:}\;&\textcolor{red}{35}x_{1}+\textcolor{red}{4}x_{2}\textcolor{red}{-15}x_{3}=\textbf{a}\end{align*}$

3.Schritt: Setze deinen Stützvektor ein

Mit dem Ansatz deiner Koordinatenform kannst du deinen Stützvektor in deine Gleichung einsetzen. Damit bestimmst du a:

$\begin{align*}\textcolor{red}{35}\cdot\textcolor{olive}{1}+\textcolor{red}{4}\cdot\textcolor{olive}{3}\textcolor{red}{-15}\cdot\textcolor{olive}{4}=\textbf{a}\end{align*}$

$\begin{align*}-13=\textbf{a}\end{align*}$

4.Schritt: Stelle die Koordinatenform auf

Nun musst du nur noch a in deinen Ansatz einsetzen und erhältst deine Koordinatenform:

$\begin{align*} \text{E:}\;& 35x_{1}+4x_{2}-15x_{3}=-13 \end{align*}$

Jetzt hast du mit nur 4 Schritten deine Parameterform in die Koordinatenform umgewandelt.

Parameterform in Koordinatenform: Aufgaben

im Videozur Stelle im Video springen

Wie du siehst, ist es gar nicht so schwer, die Parametergleichung in die Koordinatengleichung zu bringen. Mit diesen Aufgaben kannst du die einzelnen Schritte nochmal üben.

Parameterform in Koordinatenform: Aufgabe 1

Bringe die Ebene E in Koordinatenform:

$\begin{align*}\text{E:}\;&\overrightarrow{X}=\textcolor{olive}{\left(\begin{array}{c}1\\0\\0\end{array}\right)}+\lambda\textcolor{blue}{\left(\begin{array}{c}2\\0\\0\end{array}\right)}+\mu\textcolor{blue}{\left(\begin{array}{c}3\\1\\0\end{array}\right)}\end{align*}$

Mit den 4 Schritten von oben ist das kein Problem.

Lösung:

Zuerst bildest du das Kreuzprodukt aus den beiden Spannvektoren.

$\textcolor{blue}{\left(\begin{array}{c}2\\0\\0\end{array}\right)}\times\textcolor{blue}{\left(\begin{array}{c}3\\1\\0\end{array}\right)}=\left(\begin{array}{c}0\cdot0-1\cdot0\\0\cdot3-0\cdot2\\2\cdot1-3\cdot0\end{array}\right)=\textcolor{red}{\left(\begin{array}{c}0\\0\\2\end{array}\right)}$

Danach stellst du den Ansatz deiner Ebenengleichung neu auf und erhältst:

$\begin{align*}\text{E:}\;&\textcolor{red}{0}x_{1}+\textcolor{red}{0}x_{2}+\textcolor{red}{2}x_{3}=\textbf{a}\end{align*}$

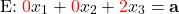
Wenn du deinen Stützvektor einsetzt, kannst du wieder a berechnen:

$\begin{align*}0\cdot\textcolor{olive}{1}+0\cdot\textcolor{olive}{0}+2\cdot\textcolor{olive}{0}=\textbf{a}\end{align*}$

$\begin{align*}0=\textbf{a}\end{align*}$

Da du a berechnet hast, kannst du deine Ebenengleichung in Koordinatenform angeben:

$\begin{align*}\text{E:}\;&2x_{3}=0\end{align*}$

Parameterform in Koordinatenform: Aufgabe 2

Bestimme die Koordinatenform der Ebenengleichung:

$\begin{align*}\text{E:}\;&\overrightarrow{X}=\textcolor{olive}{\left(\begin{array}{c}3\\2\\3\end{array}\right)}+\lambda\textcolor{blue}{\left(\begin{array}{c}4\\5\\6\end{array}\right)}+\mu\textcolor{blue}{\left(\begin{array}{c}1\\1\\1\end{array}\right)}\end{align*}$

Lösung:

Wieder musst du zuerst den Normalenvektor bilden. Dafür berechnest du das Kreuzprodukt der Spannvektoren:

$\textcolor{blue}{\left(\begin{array}{c}4\\5\\6\end{array}\right)}\times\textcolor{blue}{\left(\begin{array}{c}1\\1\\1\end{array}\right)}=\textcolor{red}{\left(\begin{array}{c}-1\\2\\-1\end{array}\right)}$

Jetzt kannst du den ersten Ansatz deiner Ebenengleichung aufstellen:

$\begin{align*}\text{E:}\;&\textcolor{red}{-1}x_{1}+\textcolor{red}{2}x_{2}\textcolor{red}{-1}x_{3}=\textbf{a}\end{align*}$

Durch das Einsetzen des Stützvektors erhältst du wieder a:

$\begin{align*}\text{E:}\;&-1\cdot\textcolor{olive}{3}+2\cdot\textcolor{olive}{2}-1\cdot\textcolor{olive}{3}=\textbf{a}\end{align*}$

$\begin{align*}2=\textbf{a}\end{align*}$

Jetzt kannst du deine Koordinatenform aufstellen, indem du a in deinen Ansatz vom vorherigen Schritt einsetzt:

$\begin{align*}\text{E:}\;&-x_{1}+2x_{2}-x_{3}=2\end{align*}$

Parameterform in Koordinatenform: Aufgabe 3

Stelle die Koordinatenform einer Ebene auf. Über die Ebene weißt du, dass sie die Punkte P₁ (2|5|5), P₂ (2|4|6) und den Koordinatenursprung O (0|0|0) beinhaltet.

Lösung:

Dieses Mal kannst du die Schritte nicht direkt anwenden. Zuerst musst du die Parameterform der Ebene aufstellen. Also bestimmst du die beiden Spannvektoren $\overrightarrow{v}$ und $\overrightarrow{u}$ . Dafür benötigst du nur die Ortsvektoren der Punkte P₁und P₂. Die Ortsvektoren entsprechen den Streckenvektoren zwischen dem Nullpunkt und den Punkten P₁und P₂.

$\overrightarrow{v}=\overrightarrow{P_{1}}-\overrightarrow{O}=\textcolor{blue}{\left(\begin{array}{c}2\\5\\5\end{array}\right)}$

$\overrightarrow{u}=\overrightarrow{P_{2}}-\overrightarrow{O}=\textcolor{blue}{\left(\begin{array}{c}2\\4\\6\end{array}\right)}$

Jetzt kannst du die Ebene in Parameterform angeben. Dabei entsprechen $\overrightarrow{v}$ und $\overrightarrow{u}$ den Spannvektoren. Deinen Stützvektor erhältst du, indem du den Ortsvektor des Ursprungs O(0|0|0) bildest.

$\begin{align*}\text{E:};&\overrightarrow{X}=\textcolor{olive}{\left(\begin{array}{c}0\\0\\0\end{array}\right)}+\lambda\textcolor{blue}{\left(\begin{array}{c}2\\5\\5\end{array}\right)}+\mu\textcolor{blue}{\left(\begin{array}{c}2\\4\\6\end{array}\right)}\end{align*}$

Jetzt kannst du wieder nach den einzelnen Schritten vorgehen und die Paramterform in die Koordinatenform umwandeln :

Berechne zuerst mit dem Kreuzprodukt der beiden Spannvektoren deinen Normalenvektor.

$\textcolor{blue}{\left(\begin{array}{c}2\\5\\5\end{array}\right)}\times\textcolor{blue}{\left(\begin{array}{c}2\\4\\6\end{array}\right)}=\textcolor{red}{\left(\begin{array}{c}10\\-2\\-2\end{array}\right)}$

Stelle nun den neuen Ansatz deiner Ebenengleichung auf.

$\begin{align*}\text{E:}\;&\textcolor{red}{10}x_{1}\textcolor{red}{-2}x_{2}\textcolor{red}{-2}x_{3}=\textbf{a}\end{align*}$

Jetzt musst du noch den Stützvektor einsetzen, um a zu bestimmen:

$10\cdot\textcolor{olive}{0}-2\cdot\textcolor{olive}{0}-2\cdot\textcolor{olive}{0}=\textbf{a}$

$0=\textbf{a}$

Wenn du zum Schluss noch a in deine Vorlage einsetzt, erhältst du die Koordinatenform:

$\begin{align*}\text{E:}\;&10x_{1}-2x_{2}-2x_{3}=0\end{align*}$

Quiz zum Thema Parameterform in Koordinatenform

Kreuzprodukt

Um die Parameterform in die Koordinatenform umzuwandeln, solltest du auch unbedingt das Kreuzprodukt draufhaben. Schaue dir doch gleich unser Video dazu an.

Zum Video: Kreuzprodukt

zur Videoseite: Parameterform in Koordinatenform

Beliebte Inhalte aus dem Bereich Geometrie

Koordinatenform

Hessesche Normalform

Ebenengleichung

Schnittgerade zweier Ebenen

Schnittpunkt Gerade Ebene

Koordinatenform in Parameterform

Parameterform in Koordinatenform

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .