Flächeninhalt
Was ist ein Flächeninhalt und wie berechnest du ihn für verschiedene Formen? Das erfährst du in diesem Artikel und in unserem Video !
Inhaltsübersicht
Flächeninhalt einfach erklärt
Für den Flächeninhalt schaust du dir immer eine Fläche an. Eine Fläche ist eine Form mit einer Länge und einer Breite, zum Beispiel ein Blatt Papier oder ein Bierdeckel. Merke dir, dass eine Fläche nie in die Höhe geht, also nicht dreidimensional ist!
In Mathe haben viele Flächen eigene Namen, zum Beispiel Rechteck, Dreieck oder Kreis.
Die Größe einer solchen Fläche nennst du Flächeninhalt. Er sagt dir zum Beispiel, wie viel Farbe du brauchst, um die Fläche auszumalen. Sieh dir gleich die Formeln an, mit denen du die Flächen für verschiedene Formen berechnen kannst!
Flächeninhalt Quadrat
Schau dir ein Quadrat an.
- Seiten: alle vier Seiten a sind gleich lang
- Winkel: alle Winkel sind 90° groß (α = β = γ = δ = 90°)
- Winkelsumme : alle Winkel sind zusammen 360° groß (α + β + γ + δ = 360°)
Den Flächeninhalt A vom Quadrat berechnest du mit der Formel:
A = a • a
Beispiel: Ein Quadrat hat die Seitenlänge a = 4 cm. Dann ist seine Fläche:
A = 4 cm • 4 cm = 16 cm2
Die Einheiten für Flächeninhalte haben meistens ein „Quadrat“ im Namen, zum Beispiel Quadratzentimeter oder Quadratmeter. Du schreibst das mit einem hoch 2, also cm2 oder m2.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Flächeninhalt Rechteck
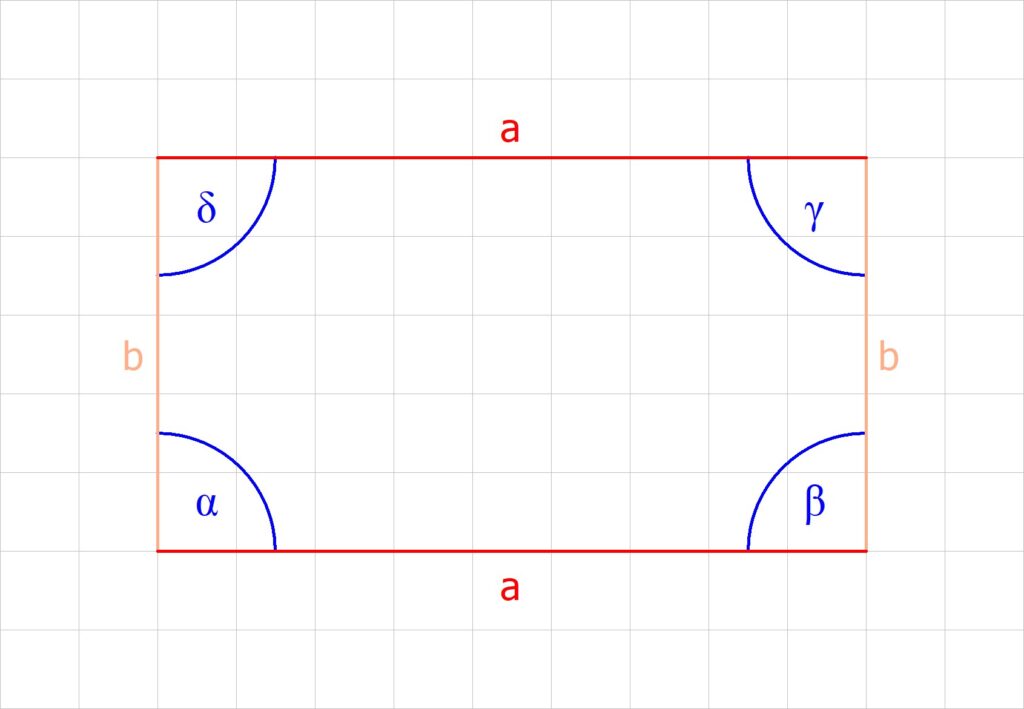
Schau dir ein Rechteck an.
- Seiten: die gegenüberliegenden Seiten sind immer gleich lang und parallel
- Winkel: alle Winkel sind 90° groß (α = β = γ = δ = 90°)
- Winkelsumme: alle Winkel sind zusammen 360° groß (α + β + γ + δ = 360°)
Der Flächeninhalt A vom Rechteck ist:
A = a • b
Beispiel: Ein Rechteck hat die Seitenlängen a = 4 cm und b = 3 cm. Dann ist seine Fläche:
A = 4 cm • 3 cm = 12 cm2
Flächeninhalt Dreieck
Schau dir jetzt ein Dreieck an.
- Seiten: die Seiten nennst du a, b und c. Sie können unterschiedlich lang sein.
- Höhe h: sie verläuft im rechten Winkel von einer Seite zu gegenüberliegenden Ecke.
- Winkelsumme: alle Winkel sind zusammen 180° groß (α + β + γ = 180°)
Die Formel für den Flächeninhalt A vom Dreieck ist:
A = 0,5 • g • h
Dabei ist g irgendeine Seite des Dreiecks (a, b oder c) und h die dazugehörige Höhe .
Beispiel: Ein Dreieck hat die Seitenlänge c = 5 cm und die dazugehörige Höhe h = 4 cm. Dann ist seine Fläche:
A = 0,5 • 5 cm • 4 cm = 10 cm2
Flächeninhalt Parallelogramm
Hier siehst du ein Parallelogramm .
- Seiten: die gegenüberliegenden Seiten sind gleich lang und parallel (a = c und b = d)
- Höhe ha: der Abstand zwischen a und c
- Winkel: die gegenüberliegenden Winkel sind gleich groß (α = γ und β = δ)
- Winkelsumme: alle Winkel sind zusammen 360° groß (α + β + γ + δ = 360°)
Den Flächeninhalt A vom Parallelogramm berechnest du mit der Formel:
A = a • ha
Beispiel: Ein Parallelogramm hat die Seitenlänge a = 5 cm und die Höhe ha = 4 cm. Dann ist seine Fläche:
A = 5 cm • 4 cm = 20 cm2
Flächeninhalt Trapez
Schau dir jetzt das Trapez an.
- Seiten: nur zwei Seiten sind parallel (a || c)
- Höhe h: der Abstand zwischen a und c
- Winkel: die zwei Winkel auf einer Seite ergeben jeweils zusammen 180° (α + δ = 180° und β + γ = 180°)
- Winkelsumme: alle Winkel sind zusammen 360° groß (α + β + γ + δ = 360°)
Die Formel für den Flächeninhalt A vom Trapez lautet:
A = 0,5 • (a + c) • h
Beispiel: Ein Trapez hat die Seitenlängen a = 5 cm, c = 3 cm und die Höhe h = 4 cm. Dann ist seine Fläche:
A = 0,5 • (5 cm + 3 cm) • 4 cm = 16 cm2
Flächeninhalt Raute
Hier siehst du eine Raute .
- Seiten: alle Seiten sind gleich lang (a = b = c = d) und gegenüberliegende Seiten sind parallel (a || c und b || d)
- Höhe h: der Abstand von zwei parallelen Seiten
- Winkel: gegenüberliegende Winkel sind gleich groß (α = γ und β = δ)
- Winkelsumme: alle Winkel sind zusammen 360° groß (α + β + γ + δ = 360°)
Den Flächeninhalt A der Raute berechnest du so:
A = a • h
Beispiel: Eine Raute hat die Seitenlänge a = 5 cm und die Höhe h = 4 cm. Dann ist seine Fläche:
A = 5 cm • 4 cm = 20 cm2
Flächeninhalt Kreis
Schau dir zum Schluss noch einen Kreis an.
- Mittelpunkt M: der Punkt genau in der Mitte vom Kreis. Er hat von allen Punkten auf der Kreislinie den gleichen Abstand
- Radius r: der Abstand vom Mittelpunkt zur Kreislinie
- Durchmesser d: der größtmögliche Abstand von zwei Punkten auf der Kreislinie. Er ist doppelt so groß wie der Radius.
Die Formel für den Flächeninhalt A vom Kreis lautet:
A = π • r2
π (Pi) ist dabei eine feste Zahl und ungefähr 3,14 groß.
Beispiel: Ein Kreis hat einen Radius von r = 4 cm. Dann ist seine Fläche:
A = π • (4 cm)2 = 50,27 cm2
Flächeninhalte zusammensetzte Flächen
Oft haben Flächen aber nicht nur eine der Formen, für die du eine Formel kennst. Du sprichst dann von zusammengesetzten Flächen. Schau dir dazu ein Beispiel an:
Hier gehst du so vor:
- Schritt 1: Zerlege die Figur in Formen, die du kennst. In diesem Fall ist das zum Beispiel ein Quadrat und ein Dreieck.
- Schritt 2: Berechne die Flächeninhalte der einzelnen Figuren.
AQuadrat = 4 cm • 4 cm = 16 cm2
ADreieck = 0,5 • 4 cm • 2 cm = 4 cm2
- Schritt 3: Zähle die einzelnen Flächeninhalte zusammen:
A = 16 cm2 + 4 cm2 = 20 cm2
Prima! Die gesamte Figur hat also eine Fläche von 20 cm2.
Übrigens: Die Zerlegung in verschiedene bekannte Flächeninhalte ist nicht eindeutig. Im Beispiel oben hättest du deine Figur zum Beispiel auch in zwei Trapeze zerlegen können.
Schau dir jetzt noch an, was es mit Flächeninhalt und Umfang auf sich hat!
Flächeninhalt — häufigste Fragen
(ausklappen)
Flächeninhalt — häufigste Fragen
(ausklappen)-
Wie erkenne ich schnell, welche Flächenform ich vor mir habe?Du erkennst die Flächenform am schnellsten an typischen Merkmalen wie parallelen Seiten, rechten Winkeln und gleich langen Seiten. Ein Trapez hat genau ein Paar paralleler Seiten, ein Parallelogramm zwei Paare, ein Rechteck vier rechte Winkel und ein Kreis hat überall den gleichen Abstand zum Mittelpunkt.
-
Wie finde ich die richtige Höhe im Dreieck, wenn sie schräg liegt?Die richtige Höhe im Dreieck ist immer die Strecke, die senkrecht (im 90°-Winkel) auf der gewählten Grundseite steht. Liegt die Höhe „schräg“, verlängerst du die Grundseite gedanklich, bis du das Lot fällen kannst. Beispiel: Bei einem stumpfwinkligen Dreieck liegt der Fußpunkt der Höhe oft außerhalb des Dreiecks.
-
Welche Fehler passieren oft beim Flächeninhalt von Trapezen?Häufige Fehler beim Trapez sind: falsche Seiten addieren (es zählen nur die beiden parallelen Seiten), die schräge Seite als Höhe nehmen und die Klammer vergessen. Beispiel: Richtig ist
 ; falsch wäre
; falsch wäre  , weil dann nicht zuerst addiert wird.
, weil dann nicht zuerst addiert wird.
-
Wann muss ich bei zusammengesetzten Flächen etwas abziehen statt addieren?Du musst bei zusammengesetzten Flächen abziehen, wenn eine Teilfläche in der Gesamtfigur fehlt oder „ausgeschnitten“ ist, also ein Loch oder eine Aussparung bildet. Addieren passt nur, wenn die Teilflächen ohne Überlappung zusammen die ganze Figur füllen. Beispiel: Ein Rechteck mit einem ausgeschnittenen Kreis wird als Rechteckfläche minus Kreisfläche gerechnet.
-
Wie rechne ich Flächeneinheiten wie cm² in m² um?Beim Umrechnen von Flächeneinheiten wird der Umrechnungsfaktor quadriert, weil es um „Länge mal Breite“ geht. Von
 zu
zu  teilst du durch
teilst du durch  , denn
, denn  . Beispiel:
. Beispiel:  sind
sind  .
.
Flächeninhalt und Umfang
Du kennst dich nun bestens mit Flächen in Mathe aus! Aber was ist eigentlich der Unterschied zwischen Flächeninhalt und Umfang?
Mit dem Flächeninhalt misst du die Größe der Fläche einer Figur, zum Beispiel eines Rechtecks. Beim Umfang dagegen rechnest du alle Seiten der Figur zusammen (Summe der Seitenlängen). Er ist also die Länge der Linie um die Figur herum (Begrenzungslinie).
Du willst mehr über den Umfang erfahren? Dann schau dir gleich unser Video zum Umfang vom Rechteck an. Viel Spaß!