Video

Quiz

Hier geht's zum Video „Parameterform“

Hier geht's zum Video „Richtungsvektor“

Hier geht's zum Video „Lineare Unabhängigkeit und lineare Abhängigkeit von Vektoren“

Hier geht's zum Video „Normalenform“

Hier geht's zum Video „Normalenvektor“

Hier geht's zum Video „Parameterform in Koordinatenform“

Hier geht's zum Video „Koordinatenform in Parameterform“

Ebenengleichung

Wichtige Inhalte in diesem Video

Ebenengleichung einfach erklärt

Ebenengleichung umformen

Du willst wissen, was eine Ebenengleichung ist und wie du die verschiedenen Formen ineinander umwandelst? Hier und im Video erfährst du alles, was du dazu wissen musst!

Inhaltsübersicht

Ebenengleichung einfach erklärt

im Videozur Stelle im Video springen

Eine Ebenengleichung ist die Darstellung einer flachen Ebene in einem dreidimensionalen Koordinatensystem. Allgemein wird eine Ebene in der Parameterform abgebildet:

$E: \vec{x} = \textcolor{orange}{\vec{a}} + r \cdot \textcolor{blue}{\vec{u}} + s \cdot \textcolor{blue}{\vec{v}}$

Du kannst eine Ebene aber auch mit der Normalenform darstellen:

$E\colon \textcolor{red}{\vec{n}} \cdot (\vec{x} - \textcolor{orange}{\vec{p}})= 0$

Multiplizierst du die Normalenform aus, dann erhältst du die Koordinatenform:

$E: \textcolor{red}{a}x_1+ \textcolor{red}{b}x_2+ \textcolor{red}{c}x_3= d$

Wie du eine Parameterform aufstellst und wie du die drei Formen der Ebenengleichung ineinander umwandeln kannst, erfährst du in den folgenden Kapiteln.

Definition einer Ebene

Eine Ebene kann durch drei Punkte oder einen Punkt und zwei linear unabhängige Richtungsvektoren eindeutig bestimmt werden. Dadurch kann eine Ebene mit unterschiedlichen Ebenengleichungen analytisch beschrieben werden.

Parameterform

Die Parameterform ist eine allgemeine Darstellungsform einer Ebene. Du brauchst dafür einen Stützvektor $\textcolor{orange}{\vec{a}}$ und zwei Richtungsvektoren $\textcolor{blue}{\vec{u}}$ und $\textcolor{blue}{\vec{v}}$ . Du erkennst einen Richtungsvektor immer daran, dass eine Variable wie s, t oder r davor steht. Ein Beispiel könnte so aussehen:

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} 0 \\ 3 \\ 1 \end{array}\right)} + r \cdot \textcolor{blue}{\left(\begin{array}{c} -1 \\ -3 \\ 1 \end{array}\right)} + s \cdot \textcolor{blue}{\left(\begin{array}{c} -1 \\ 1 \\ 0,5 \end{array}\right)}$

Ebenengleichung, Ebenengleichungen, Ebenengleichung aufstellen, Ebenengleichung umformen, Ebenengleichung umwandeln, Ebenengleichung in Parameterform, Parameterform, Ebene im Raum, Vektor Ebene — Parameterform

Merke: Die Richtungsvektoren einer Ebene dürfen kein Vielfaches voneinander sein. Das solltest du überprüfen, sonst erhältst du die Gleichung einer Geraden.

Expertenwissen zur Parameterform

Du kannst die Gleichung auch umstellen zu $\vec{x}$ – $\textcolor{orange}{\vec{a}}$ = $r \cdot \vec{b} - \textcolor{orange}{\vec{a}}$ + $s \cdot \vec{c} - \textcolor{orange}{\vec{a}}$ . So lässt sich $\vec{x}$ – $\textcolor{orange}{\vec{a}}$ als Linearkombination der Vektoren $\textcolor{blue}{\vec{u}}$ : = $\vec{b}$ – $\textcolor{orange}{\vec{a}}$ und $\textcolor{blue}{\vec{v}}$ : = $\vec{c}$ − $\textcolor{orange}{\vec{a}}$ eindeutig darstellen.

Normalenform

Eine Ebenengleichung kannst du auch in der Normalenform angeben. Dafür brauchst du den Normalenvektor $\textcolor{red}{\vec{n}}$ und einen Stützvektor $\textcolor{orange}{\vec{p}}$ :

$E\colon \textcolor{red}{\left(\begin{array}{c} 3 \\ -4 \\ 1 \end{array}\right)} \cdot \left( \textcolor{blue}{\left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)} - \textcolor{orange}{\left(\begin{array}{c} 0 \\ -0,5 \\ 0 \end{array}\right)} \right) = 0$

Merke: Ein Normalenvektor verläuft immer senkrecht zu beiden Richtungsvektoren der Ebene.

Ebenengleichung, Ebenengleichungen, Ebenengleichung aufstellen, Ebenengleichung umformen, Ebenengleichung umwandeln, Ebenengleichung Normalenform, Normalenform, Ebene im Raum, Vektor Ebene — Normalenform

Möchtest du den Normalenvektor berechnen, dann kannst du das Kreuzprodukt aus den beiden Richtungsvektoren $\vec{u}$ x $\vec{v}$ bestimmen oder aus der Koordinatenform ablesen. Die Koordinaten des Normalenvektors findest du dabei als Zahlen vor x₁, x₂ und x₃.

Expertenwissen: Hessesche Normalenform

Normierst du den Normalenvektor zu $\vec{n_0}$ , dann kannst du die Ebenengleichung in der Hesseschen Normalenform angeben: $E: \vec{n_0} \cdot (\vec{x} - \vec{a}) = 0$ . Den normierten Normalenvektor bestimmst du so:

$\vec{n_0} = \frac{\vec{n}}{\left| \vec{n} \right|}$

Koordinatenform

Multiplizierst du die Normalenform aus, bekommst du die Koordinatenform :

$E: \textcolor{red}{3}x_1 \textcolor{red}{- 4}x_2 + \textcolor{red}{1}x_3 = 2$

Merke: Die Zahlen vor x₁, x₂ und x₃ sind die Koordinaten des Normalenvektors. Die Zahl hinter dem Gleichheitszeichen entsteht durch die Multiplikation des Normalenvektors mit dem Stützvektor.

$d = \textcolor{red}{\vec{n}} \cdot \textcolor{orange}{\vec{p}} = \textcolor{red}{\left(\begin{array}{c} 3 \\ -4 \\ 1 \end{array}\right)} \cdot \textcolor{orange}{\left(\begin{array}{c} 0 \\ -0,5 \\ 0 \end{array}\right)} \right) = 2$

Expertenwissen zur Normalenform und Koordinatenform

Durch die Koordinatenform und die Normalenform werden alle Punkte des Raumes beschrieben, die dieselbe Normalprojektion des zugehörigen Ortsvektors in Richtung des Normalenvektors besitzen. Alle beschriebenen Punkte bilden eine Ebene, auf der der Normalenvektor senkrecht steht.

Ebenengleichung aufstellen

Du kannst eine Ebenengleichung in Parameterform auf vier unterschiedliche Arten aufstellen: mit drei Punkten, einer Geradengleichung und einem Punkt, zwei parallelen Geraden und zwei sich schneidenden Geraden. Die Vorgehensweise wird dir in den folgenden Kapiteln erklärt.

Ebenengleichung aufstellen — 3 Punkte

Du hast die drei Punkte A(0|3|1), B(-1|0|2) und C(-1|4|1,5) gegeben. Mit ihnen kannst du in nur drei Schritten eine Ebenengleichung in Parameterform aufstellen:

Ortsvektor als Stützvektor bestimmen: Wähle einen beliebigen Ortsvektor eines Punktes, zum Beispiel OA, aus. Dieser ist der Stützvektor der Ebene.

$\textcolor{orange}{\vec{a}} = \vec{OA} = \textcolor{orange}{\left(\begin{array}{c} 0 \\ 3 \\ 1 \end{array}\right)}$
Richtungsvektoren berechnen: Berechne dann zwei Richtungsvektoren, zum Beispiel AB und AC.

$\textcolor{blue}{\vec{u}} = \vec{AB} = \left(\begin{array}{c} -1 - 0 \\ 0 - 3 \\ 2 - 1 \end{array}\right) = \textcolor{blue}{\left(\begin{array}{c} -1 \\ -3 \\ 1 \end{array}\right)}$ $\textcolor{blue}{\vec{v}} = \vec{AC} = \left(\begin{array}{c} -1 - 0 \\ 4 - 3 \\ 1,5 - 1 \end{array}\right) = \textcolor{blue}{\left(\begin{array}{c} -1 \\ 1 \\ 0,5 \end{array}\right)}$
Ebenengleichung zusammenstellen: Füge als letztes die ganzen Bestandteile zu einer Gleichung zusammen.

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} 0 \\ 3 \\ 1 \end{array}\right)} + r \cdot \textcolor{blue}{ \left(\begin{array}{c} -1 \\ -3 \\ 1 \end{array}\right)} + s \cdot \textcolor{blue}{\left(\begin{array}{c} -1 \\ 1 \\ 0,5 \end{array}\right)}$

Ebenengleichung aufstellen — Gerade und Punkt außerhalb

Du kannst eine Parameterform auch mithilfe einer Gerade und einem Punkt, der nicht auf der Geraden liegt, bestimmen:

$g: \vec{x} = \left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right) + r \cdot \left(\begin{array}{c} 5 \\ 1 \\ 2 \end{array}\right)$ und P(2|2|1)

Stützvektor und Richtungsvektor der Geraden übernehmen: Schreibe den Stützvektor und den Richtungsvektor der Geradengleichung in Parameterform in die Ebenengleichung.

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right)} + r \cdot \textcolor{blue}{\left(\begin{array}{c} 5 \\ 1 \\ 2 \end{array}\right)} + s \cdot \vec{v}$
Zweiten Richtungsvektor berechnen: Berechne aus dem Stützvektor und dem Punkt P einen zweiten Richtungsvektor $\textcolor{blue}{\vec{v}}$ , der die Ebene aufspannt.

$\textcolor{blue}{\vec{v}} = \vec{a} - \vec{OP} = \left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right) - \left(\begin{array}{c} 2 \\ 2 \\ 1 \end{array}\right) = \textcolor{blue}{\left(\begin{array}{c} 1 \\ 0 \\ 1 \end{array}\right)}$
Ebenengleichung zusammenstellen: Füge jetzt den zweiten Richtungsvektor in die Ebenengleichung ein.

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right)} + r \cdot \textcolor{blue}{\left(\begin{array}{c} 5 \\ 1 \\ 2 \end{array}\right)} + s \cdot \textcolor{blue}{\left(\begin{array}{c} 1 \\ 0 \\ 1 \end{array}\right)}$

Ebenengleichung aufstellen — zwei parallele Geraden

Auch aus zwei parallelen Geraden kannst du eine Ebenengleichung in Parameterform aufstellen:

$g: \vec{x} = \left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right) + r \cdot \left(\begin{array}{c} 3 \\ -1 \\ 2 \end{array}\right)$ und $h: \vec{x} = \left(\begin{array}{c} 0 \\ 1 \\ 3 \end{array}\right) + t \cdot \left(\begin{array}{c} -6 \\ 2 \\ -4 \end{array}\right)$

Stützvektor und Richtungsvektor einer Geraden übernehmen: Such dir zum Beispiel die Gerade g aus und übertrage ihren Stützvektor und Richtungsvektor in die Ebenengleichung:

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right)} + r \cdot \textcolor{blue}{\left(\begin{array}{c} 3 \\ -1 \\ 2 \end{array}\right)} + s \cdot \vec{v}$
Zweiten Richtungsvektor aus den beiden Stützvektoren der Geraden berechnen: Berechne aus den Stützvektoren von g und h einen Verbindungsvektor.

$\textcolor{blue}{\vec{v}} = \vec{a} - \vec{b} = \left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right) - \left(\begin{array}{c} 0 \\ 1 \\ 3 \end{array}\right)$

$\textcolor{blue}{\vec{v}} = \textcolor{blue}{\left(\begin{array}{c} 3 \\ 1 \\ -1 \end{array}\right)}$
Ebenengleichung zusammensetzen: Füge den Stützvektor in die Ebenengleichung ein:

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right)} + r \cdot \textcolor{blue}{\left(\begin{array}{c} 3 \\ -1 \\ 2 \end{array}\right)} + s \cdot \textcolor{blue}{\left(\begin{array}{c} 3 \\ 1 \\ -1 \end{array}\right)}$

Ebenengleichung aufstellen — zwei sich schneidende Geraden

Die letzte Möglichkeit eine Ebenengleichung in Parameterform aufzustellen, sind zwei sich schneidende Geraden:

$g: \vec{x} = \left(\begin{array}{c} -3 \\ -4 \\ 1 \end{array}\right) + r \cdot \left(\begin{array}{c} 2 \\ 2 \\ 1 \end{array}\right)$ und $h: \vec{x} = \left(\begin{array}{c} 4 \\ 3 \\ 1 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ -1 \\ 1 \end{array}\right)$

Stützvektor und Richtungsvektor einer Geraden übernehmen: Auch hier kannst du eine Geradengleichung, zum Beispiel wie die von g, in die Ebenengleichung übertragen.

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} -3 \\ -4 \\ 1 \end{array}\right)} + r \cdot \textcolor{blue}{\left(\begin{array}{c} 2 \\ 2 \\ 1 \end{array}\right)} + s \cdot \vec{v}$
Richtungsvektor der anderen Gerade g als zweiten Richtungsvektor der Ebene nehmen: In diesem Fall brauchst du keinen neuen Vektor berechnen, sondern kannst den Richtungsvektor der zweiten Gerade h einsetzen.

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} -3 \\ -4 \\ 1 \end{array}\right)} + r \cdot \textcolor{blue}{\left(\begin{array}{c} 2 \\ 2 \\ 1 \end{array}\right)} + s \cdot \textcolor{blue}{\left(\begin{array}{c} -1 \\ -1 \\ 1 \end{array}\right)}$

Ebenengleichung umformen

im Videozur Stelle im Video springen

Die drei Ebenengleichungen kannst du ineinander umwandeln. Manchmal ist es praktischer mit einer bestimmten Form weiterzurechnen oder die Aufgabenstellung schreibt es dir vor.

Parameterform in Normalenform

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} 0 \\ 3 \\ 1 \end{array}\right)} + r \cdot \textcolor{blue}{\left(\begin{array}{c} -1 \\ -3 \\ 1 \end{array}\right)} + s \cdot \textcolor{blue}{\left(\begin{array}{c} -1 \\ 1 \\ 0,5 \end{array}\right)}$

Normalenvektor mit dem Kreuzprodukt der beiden Richtungsvektoren berechnen:

$\textcolor{red}{\vec{n}} = \vec{u} \times \vec{v} = \textcolor{blue}{\left(\begin{array}{c} -1 \\ -3 \\ 1 \end{array}\right)} \times \textcolor{blue}{\left(\begin{array}{c} -1 \\ 1 \\ 0,5 \end{array}\right)} = \textcolor{red}{\left(\begin{array}{c} -2,5 \\ -0,5 \\ -4 \end{array}\right)}$
Stützvektor aus Parameterform übernehmen: $\textcolor{orange}{\vec{p}} = \textcolor{orange}{\left(\begin{array}{c} 0 \\ 3 \\ 1 \end{array}\right)}$
Vektoren in Normalenform einsetzen:

$E\colon \textcolor{red}{\left(\begin{array}{c} -2,5 \\ -0,5 \\ -4 \end{array}\right)} \cdot \left( \textcolor{blue}{\left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)} - \textcolor{orange}{\left(\begin{array}{c} 0 \\ 3 \\ 1 \end{array}\right)} \right) = 0$

Normalenform in Parameterform

$E\colon \textcolor{red}{\left(\begin{array}{c} 3 \\ -4 \\ 1 \end{array}\right)} \cdot \left( \textcolor{blue}{\left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)} - \textcolor{orange}{\left(\begin{array}{c} 0 \\ -0,5 \\ 0 \end{array}\right)} \right) = 0$

Stützvektor übernehmen: $\textcolor{orange}{\vec{a}} = \textcolor{orange}{\left(\begin{array}{c} 0 \\ -0,5 \\ 0 \end{array}\right)} \right)$
Suche zwei Richtungsvektoren, die senkrecht zum Normalenvektor stehen:

$\textcolor{blue}{\vec{u}} = \left(\begin{array}{c} 0 \\ - n_3 \\ n_2 \end{array}\right) = \textcolor{blue}{\left(\begin{array}{c} 0 \\ - 1 \\ -4 \end{array}\right)}$ und $\textcolor{blue}{\vec{v}} = \left(\begin{array}{c} n_2 \\ - n_1 \\ 0 \end{array}\right) = \textcolor{blue}{\left(\begin{array}{c} -4 \\ -3 \\ 0 \end{array}\right)}$
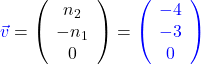
Vektoren in die Parameterform einsetzen:

$E: \vec{x} = \textcolor{orange}{\left(\begin{array}{c} 0 \\ -0,5 \\ 0 \end{array}\right)} \right) + r \cdot \textcolor{blue}{\left(\begin{array}{c} 0 \\ - 1 \\ -4 \end{array}\right)} + s \cdot \textcolor{blue}{\left(\begin{array}{c} -4 \\ -3 \\ 0 \end{array}\right)}$

Normalenform in Koordinatenform

$E\colon \textcolor{red}{\left(\begin{array}{c} 3 \\ -4 \\ 1 \end{array}\right)} \cdot \left( \textcolor{blue}{\left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)} - \textcolor{orange}{\left(\begin{array}{c} 0 \\ -0,5 \\ 0 \end{array}\right)} \right) = 0$

Normalenform ausmultiplizieren:
E: 3 · x₁ – 4 · x₂ + 1 · x₃ + 3 · 0 – 4 · 0,5 + 1 · 0 = 0
E: 3x₁ – 4x₂ + x₃ – 2 = 0
Zahlen ohne x Variable auf die andere Seite des Gleichheitszeichens bringen:
E: 3x₁ – 4x₂ + x₃ = 2

Koordinatenform in Normalenform

E: 3x₁ – 4x₂ + x₃ = 2

Normalenvektor ablesen:

$\textcolor{red}{\vec{n}} = \textcolor{red}{\left(\begin{array}{c} 3 \\ -4 \\ 1 \end{array}\right)}$
Stützvektor finden: Dafür wählst du zwei x-Variablen frei aus, zum Beispiel x₂ = x₃ = 0. Die setzt du in die Koordinatenform ein und löst nach x₁ auf.

3x₁ = 2 | : 3

x₁ = $\frac{2}{3}$

$\textcolor{orange}{\vec{p}} = \textcolor{orange}{\left(\begin{array}{c} \frac{2}{3} \\ 0 \\ 0 \end{array}\right)} \right)$
Vektoren in Normalenform einsetzen:

$E\colon \textcolor{red}{\left(\begin{array}{c} 3 \\ -4 \\ 1 \end{array}\right)} \cdot \left( \textcolor{blue}{\left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)} - \textcolor{orange}{\left(\begin{array}{c} \frac{2}{3} \\ 0 \\ 0 \end{array}\right)} \right) = 0$

Übrigens: Du kannst auch die Parameterform in Koordinatenform oder andersherum die Koordinatenform in Parameterform umwandeln.

Ebenengleichung — häufigste Fragen

Was ist eine Ebenengleichung?
Eine Ebenengleichung ist eine Angabe der Ebene E im dreidimensionalen Raum. Du kannst mit einer Ebenengleichung bestimmen, wo die Ebene startet und in welche Richtungen sie aufgespannt wird.
Was ist eine Normalenform einer Ebene?
Eine Normalenform ist eine Darstellungsform einer Ebene. Um sie aufzustellen, brauchst du den Normalenvektor und einen Stützvektor.

Quiz zum Thema Ebenengleichung

Parameterform in Koordinatenform

Super! Du weißt jetzt, was eine Ebenengleichung ist und welche Formen es gibt. Willst du dir nochmal genauer anschauen, wie du die Parameterform in Koordinatenform umwandelst? Dann klick in unser Video rein!

Zum Video: Parameterform in Koordinatenform

zur Videoseite: Ebenengleichung

Beliebte Inhalte aus dem Bereich Geometrie

Koordinatenform

Hessesche Normalform

Ebenengleichung

Schnittgerade zweier Ebenen

Schnittpunkt Gerade Ebene

Koordinatenform in Parameterform

Parameterform in Koordinatenform

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .