Terme vereinfachen Übungen
Du wiederholst gerade Terme und suchst noch nach ein paar Übungen zum Terme vereinfachen? Dann bist du hier und im Video genau richtig. Wir zeigen dir verschiedene Aufgaben und wie du sie löst.
Inhaltsübersicht
Terme vereinfachen Übungen
Vereinfache den Term so weit wie möglich.
-
- 2x2 + 3x3 + 4x2
- 5a4 − 2b + 3a4
- 7y2 + 5y − 2y3
- 4m4 − 2m4 + 5m + 3m4
- 9c3 +3c − c3 + 2c3
- 2d2 − d2 + 4d − 3d + 7d3 + 4d2
Lösungen
Das Kommutativgesetz besagt, dass die Reihenfolge der Zahlen vertauscht werden kann, ohne dass sich das Ergebnis ändert. Achte dabei darauf, die Vorzeichen immer mitzunehmen!
Dann fasst du die Zahlen mit den gleichen Variablen zusammen, indem du die Koeffizienten miteinander verrechnest.
-
-
2x2 + 3x3 + 4x2
= 2x2 + 4x2 + 3x3
= 6x2 + 3x3
-
5a4 − 2b + 3a4
= 5a4+ 3a4− 2b
= 8a4− 2b
-
7y2 + 5y − 2y3
= − 2y3 + 7y2 + 5y
-
4m4 − 2m4 + 5m + 3m4
= 4m4 − 2m4+ 3m4 + 5m
= 5m4 + 5m
-
9c3 + 3c − c3 + 2c3
= 9c3 − c3 + 2c3 + 3c
= 10c3 + 3c
- 2d2 − d2 + 4d − 3d + 7d3 + 4d2
= 7d3 + 2d2 − d2 + 4d2 + 4d − 3d
= 7d3 + 5d2 + 1d
-
2x2 + 3x3 + 4x2
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Terme vereinfachen — Potenzen zusammenfassen
Vereinfache die Terme, indem du die Potenzen zusammenfasst.
-
- 3m2 • 2m3 + m5
- 8c4 − 2c2 • 4c
- 9d • 3d2 − 6d3
- 2x2 • 3y3 + 4x • y
- 5a • 2a2 − 3a4 • b
- 6y3 + 2z • z2 − z3
Lösungen
Bei der Multiplikation von Variablen verrechnest du zuerst die Koeffizienten miteinander.
Dann fasst du die Potenzen zusammen, indem du die Exponenten der Basis addierst. Das geht allerdings nur, wenn die Basen gleich sind! → an · am = an+m
-
-
3m2 • 2m3 + m5
=(3 • 2) • m2+3 + m5
= 6m5 + m5
= 7m5
- 8c4 − 2c2 • 4c
= 8c4 − (2 • 4) • c2+1
= 8c4 − 8c3
-
9d • 3d2 − 6d3
= (9 • 3) • d1+2 − 6d3
= 27d3 − 6d3
= 21d3
-
2x2 • 3y3 + 4x • y
= (2 •3) • x2 • y3 + (4 • 1) • x • y
= (2 •3) • x2y3 + (4 • 1) • xy
= 6x2y3 + 4xy
-
5a • 2a2 − 3a4 • b
= (5 • 2) • a • a2 − (3 • 1) • a4 • b
= (5 • 2) • a1+2 − (3 • 1) • a4b
= 10a3 − 3a4b
-
6y3 + 2z • z2 − z3
= 6y3 + (2 • 1) • z • z2 − z3
= 6y3 + (2 • 1) • z1+2 − z3
= 6y3 + (2 • 1) • z3 − z3
= 6y3 + 2z3 − z3
= 6y3 + z3
-
3m2 • 2m3 + m5
Therme vereinfachen — Klammern auflösen
Vereinfache folgende Terme, indem du die Klammern auflöst.
-
- 3x(y + 2)
- 4a(2b − 3)
- 5m(n + 4p)
- 2x(3y + 4z − 5)
- 4a(5b − 2c + 3d)
- 3m(2n + 4p − 6m)
Lösungen
Um die Klammern aufzulösen, wendest du das Distributivgesetz an. Es besagt, dass du einen Faktor außerhalb der Klammer mit jeder Zahl innerhalb der Klammer multiplizierst. Du bezeichnest es auch als Verteilungsgesetz, weil du den Faktor „verteilst“. → a • (b + c) = a • b + a • c
-
-
3x(y + 2)
= 3x • y + 3x • 2
= 3xy + 6x
-
4a(2b − 3)
= 4a • 2b + 4a • (− 3)
= 8ab − 12a
-
5m(n + 4p)
= 5m • n + 5m • 4p
= 5mn + 20mp
-
2x(3y + 4z − 5)
= 2x • 3y + 2x • 4z + 2x • (−5)
= 6xy + 8xz − 10x
-
4a(5b − 2c + 3d)
= 4a • 5b + 4a • (−2c) + 4a • 3d
= 20ab − 8ac + 12ad
-
3m(2n + 4p − 6m)
= 3m • 2n + 3m • 4p + 3m • (−6m)
= 6mn + 12mp − 18m
-
3x(y + 2)
Terme vereinfachen — Ausklammern
Vereinfache den Term durch Ausklammern.
-
- 6xy + 9x
- 8a2b − 4ab2
- 12mn − 18m2
- 12x2y + 18xy2 − 24xy
- 15a3b − 10a2b2 + 5ab
- 20m2n − 25mn2 + 30mn
Lösungen
Ausklammern hilft dir Terme zu vereinfachen, indem du den größten gemeinsamen Faktor findest und „herausziehst“. Das bedeutet, dass du den Faktor vor die Klammer setzt und in der Klammer das übrig gebliebene schreibst.
Das Prinzip basiert auf dem Distributivgesetz, das besagt, dass ein gemeinsamer Faktor vor die Klammer geschrieben werden kann. → ab + ac = a(b + c)
-
-
6xy + 9x → gemeinsamer Faktor 3x
= 3x(2y + 3)
-
8a2b − 4ab2 → gemeinsamer Faktor 4ab
= 4ab(2a − b)
-
12mn − 18m2 → gemeinsamer Faktor 6m
= 6m(2n − 3m)
- 12x2y + 18xy2 − 24xy → gemeinsamer Faktor 6xy
= 6xy(2x + 3y − 4)
-
15a3b − 10a2b2 + 5ab → gemeinsamer Faktor 5ab
= 5ab(3a2 − 2ab + 1)
-
20m2n − 25mn2 + 30mn → gemeinsamer Faktor 5mn
= 5mn(4m − 5n + 6)
-
6xy + 9x → gemeinsamer Faktor 3x
Terme vereinfachen — Brüche
Vereinfache folgende Terme mit Brüchen.
Lösungen
Um Terme mit Brüchen zu vereinfachen, kürzt du Brüche so weit wie möglich und fasst sie zusammen. Dazu hast du verschiedene Möglichkeiten:
-
Brüche vereinfachen:
Vereinfache einzelne Brüche, indem du den Zähler und den Nenner durch ihren größten gemeinsamen Teiler
teilst.
-
Gemeinsamen Nenner finden: Wenn du zwei oder mehr Brüche addieren
oder subtrahieren
musst, finde einen gemeinsamen Nenner. Dann erweiterst
oder kürzt
du die Brüche, sodass der gemeinsame Nenner unter dem Bruchstrich steht.
- Brüche verrechnen: Bei Addition und Subtraktion verrechnest du die Zähler miteinander, während der Nenner gleich bleibt. Bei Multiplikation rechnest du „Zähler mal Zähler“ und „Nenner mal Nenner“. Dividierst du Brüche, bildest du den Kehrwert eines Bruchs und multiplizierst ihn dann mit dem anderen.
-

=
=
= x
-

=
=
=
-

=
=
=
=
-
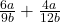
=
=
=
-

=
=
=
-

=
=
=
=
Terme vereinfachen — binomische Formeln
Vereinfache die Terme. Achte auf die binomischen Formeln!
-
- (x + 3)2
- (2a − 4)2
- (m + n)(m − n)
-
(4a − 5b)2
- (2x – 3)2 – 2 • (x + 3)2
- (x + 2)2 − (x − 3)2
Lösungen
Die binomischen Formeln sind spezielle Regeln, die dir helfen, bestimmte Terme zu vereinfachen. Bei Termen, die in folgenden drei Formen stehen, gehst du immer gleich vor:
- 1. binomische Formel: (a + b)² = a² + 2ab + b²
- 2. binomische Formel: (a – b)² = a² – 2ab + b²
- 3. binomische Formel: (a + b) • (a – b) = a² – b²
-
-
(x + 3)2
= x2 + 2 • x • 3 + 32
= x2 + 6x + 9
-
(2a − 4)2
= (2a)2 − 2 • 2a • 4 + 42
= 4a2 − 16a + 16
-
(m + n)(m − n)
= m2 – n2 -
(4a−5b)2
= (4a)2 – 2 • 4a • 5b + (5b)2
= 16a2 – 40ab + 25b2
- (2x – 3)2 – 2 • (x+3)2
= ((2x)2−2 • 2x • 3 + 32) – 2 • (x2 + 2 • x • 3 + 32)
= (4x2 − 12x + 9) – 2 • (x2 + 6x + 9)
= (4x2 − 12x + 9) − (2x2 + 12x + 18)
= 4x2 − 12x + 9 − 2x2 − 12x − 18)
= 4x2 − 2x2 − 12x − 12x + 9 − 18
= 2x2 − 24x − 9
-
(x + 2)2 − (x − 3)2
= (x2 + 4x + 4) – (x2 − 6x + 9)
= x2 +4x +4 − x2 + 6x − 9
= x2 − x2 + 4x + 6x + 4 − 9
= 10x − 5
-
(x + 3)2
Vereinfache den Term
Vereinfache die Terme. Achte dabei auf besondere Regeln und Gesetze, die dir beim Zusammenfassen der Terme helfen können.
-
- 2x3 • 4x2 • x
- 6m + 2n + 3m
- (2x + 3)2
- 6y2 − 9y
- 3x2 • 2x3y • 4y2
- 2x(3y + 4z)
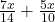
- 3(a + b)
- 10a3b − 15a2b2
- (x − 5)2
-

Lösungen
-
- Potenzen zusammenfassen
2x3 • 4x2 • x
= (2 • 4) • x3+2+1
= 8x6 - Kommutativgesetz
6m + 2n + 3m
= 6m + 3m + 2n
= 9m + 2n
- Binomische Formel
(2x + 3)2
= (2x)2 + 2 • 2x • 3 + 32
= 4x2 + 12x + 9
-
Ausklammern
6y2 − 9y
= 3y(2y − 3)
- Potenzen zusammenfassen
3x2 • 2x3y • 4y2
= (3 • 2 • 4) • x2+3 • y1+2
= 24x5y3
- Distributivgesetz
2x(3y + 4z)
= 2x • 3y + 2x • 4z
= 6xy + 8xz
- Brüche vereinfachen
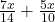
=
=
= x - Distributivgesetz
3(a + b)
= 3 • a + 3 • b
= 3a + 3b
- Ausklammern
10a3b − 15a2b2
= 5a2b(2a − 3b)
- Binomische Formel
(x − 5)2
= x2 − 2 • x • 5 + 52
= x2 − 10x + 25
- Brüche vereinfachen

=
=
=
- Potenzen zusammenfassen
Terme vereinfachen Übungen — häufigste Fragen
(ausklappen)
Terme vereinfachen Übungen — häufigste Fragen
(ausklappen)-
Wie kann man einen Term vereinfachen?
Um Terme zu vereinfachen gehst du folgendermaßen vor:
- Löse die Klammern auf. Fange immer bei der Innersten an und löse sie nach und nach bis zur Äußersten.
- Fasse Potenzen zusammen, wenn sie die gleiche Basis haben.
- Führe die Punktrechnungen durch (Multiplikation und Division)
- Löse die Strichrechnungen (Addition und Subtraktion)
-
Was ist der Unterschied zwischen Terme zusammenfassen und vereinfachen?Um Terme zusammenzufassen, werden ähnliche Termglieder miteinander kombiniert und verrechnet durch Addition, Subtraktion, Multiplikation und Division. Beim Vereinfachen von Termen werden bestimmte Regeln und Gesetze angewendet, um den Term so einfach wie möglich darzustellen.
Terme aufstellen
Super! Jetzt hast du einige Beispiele zum Thema Terme vereinfachen gerechnet. Willst du Terme auch selbstständig aufstellen können? Dann schau direkt in unserem Video dazu vorbei!
