Termumformung
Ein Term kann häufig sehr kompliziert und unübersichtlich aussehen. Wenn du ihn vereinfachen willst, kann dir eine Termumformung helfen!
Inhaltsübersicht
Termumformung einfach erklärt
Termumformungen brauchst du, wenn du einen Term übersichtlicher machen willst.
Bei einer Termumformung veränderst du einen Term, ohne sein Ergebnis zu ändern. Damit kannst du den Term vereinfachen oder nach einer Variablen auflösen.
Gleiche Variablen in einem Term kannst du zusammenfassen. Du zählst dazu einfach die einzelnen Koeffizienten zusammen. Das sind die Zahlen, die vor deinen Variablen stehen.
![Rendered by QuickLaTeX.com \[2\textcolor{red}{x}+8\textcolor{red}{x}+5\textcolor{blue}{y}+4\textcolor{blue}{y}=\underbrace{10}_{2+8}\textcolor{red}{x}+\underbrace{9}_{5+4}\textcolor{blue}{y}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6b50882c9e4283a9e75230c4976ba81c_l3.png)
Auch wenn zwei oder mehr Variablen direkt nebeneinander stehen, wie zum Beispiel bei xy, darfst du Gleiches zusammenfassen:
![Rendered by QuickLaTeX.com \[3\textcolor{red}{x}\textcolor{blue}{y}+4\textcolor{red}{x}\textcolor{blue}{y}+6=\underbrace{7}_{3+4}\textcolor{red}{x}\textcolor{blue}{y}+6\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-20e89ce121a871e35e0b49c48a427a22_l3.png)
![Rendered by QuickLaTeX.com \[2\textcolor{red}{x}\textcolor{blue}{y^2}+5\textcolor{red}{x}\textcolor{blue}{y^2}=\underbrace{7}_{2+5}\textcolor{red}{x}\textcolor{blue}{y^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d07dd3ee2d0c063e0b5852df12513008_l3.png)
Wenn gleiche Variablen miteinander multipliziert werden, zum Beispiel x und x2, fasst du diese zusammen. Dafür musst du nur die Exponenten zusammenzählen:
![Rendered by QuickLaTeX.com \[3\textcolor{red}{x}\cdot\textcolor{red}{x}^{\textcolor{olive}{2}}+10\textcolor{red}{x}\textcolor{blue}{y}^{\textcolor{olive}{2}}\cdot\textcolor{blue}{y}^{\textcolor{olive}{2}}=3\textcolor{red}{x}^{\textcolor{olive}{1}+\textcolor{olive}{2}}+10\textcolor{red}{x}\textcolor{blue}{y}^{\textcolor{olive}{2}+\textcolor{olive}{2}}=3\textcolor{red}{x}^{\textcolor{olive}{3}}+10\textcolor{red}{x}\textcolor{blue}{y}^{\textcolor{olive}{4}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9edbde6c16bacb0d9a3d77933c095aba_l3.png)
Wenn keine Zahl im Exponenten steht, bedeutet das, dass dort der Exponent einfach 1 ist. Diese lässt du normalerweise weg.
Termumformung Regeln
Es gibt natürlich noch weitere Regeln, die dir bei Termumformungen oder beim Berechnen von Termen helfen können.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Terme ausklammern
Wenn bei einer Summe oder einer Differenz in jedem Summanden die gleiche Variable vorkommt, darfst du diese ausklammern . Du musst dazu diese Variable nur vor die Klammer schreiben und bei deinen Summanden in der Klammer weglassen. Falls du eine größere Zahl als 1 im Exponenten stehen hast, zum Beispiel bei x3, ziehst du im Exponenten einfach eins ab:
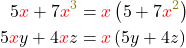
Hier bleibt x3-1, also x2, in der Klammer stehen.
Der Grund dafür ist das Distributivgesetz : Es ist egal, ob du die einzelnen Summanden mit einer Variable mal nimmst oder die ganze Summe. Das siehst du, wenn du oben für x zum Beispiel 3 einsetzt:

Terme ausmultiplizieren
Wenn du Terme ausklammern darfst, darfst du sie natürlich auch ausmultiplizieren. Dabei ziehst du deine Variable oder Zahl in die Klammer rein und multiplizierst sie mit jedem einzelnen Summanden:
![Rendered by QuickLaTeX.com \[\textcolor{red}{x}\left(2y+7x\right)=2y\cdot\textcolor{red}{x}+7x\cdot\textcolor{red}{x}=2y\textcolor{red}{x}+7\textcolor{red}{x}^2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-cabd66c00b7afb2ad04934b853fbdeeb_l3.png)
![Rendered by QuickLaTeX.com \[\textcolor{red}{3}\left(2y+7\cdot3\right)=\textcolor{red}{3}\left(2y+21\right)=\textcolor{red}{3}\cdot2y+\textcolor{red}{3}\cdot21=6y+63\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6f52c9c0ecd2b4a3655078042234bcb8_l3.png)
Wieder ändert sich nämlich der Wert des Terms nicht. Dabei darfst du keinen Summanden vergessen, ansonsten stimmt deine Rechnung nicht und der Wert deines Terms ändert sich doch. Am Besten schaust du dir dazu noch ein Zahlenbeispiel an:
![Rendered by QuickLaTeX.com \[2\cdot\left(3+4+5\right)=2\cdot3+2\cdot4+2\cdot5=24\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2c82ed49aff73457cfb8f59afe2e11f4_l3.png)
Wenn du einen Summanden vergisst, stimmt deine Rechnung nicht mehr:
![Rendered by QuickLaTeX.com \[2\cdot\left(3+4+5\right)=24\neq19=2\cdot3+2\cdot4+5\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e69a5e02cbc30176872b25dcd6d663eb_l3.png)
Terme umordnen
Wegen des Kommutativgesetzes darfst du die Reihenfolge in deinem Term bei Mal und Plus beliebig ändern. In der Summe oder im Produkt ist es egal, in welcher Reihenfolge du addierst oder mal nimmst: 4+2 ist das Gleiche wie 2+4 und 4 mal 2 ist das Gleiche wie 2 mal 4. Natürlich gilt das auch, wenn dein Term länger ist und Variablen enthält:
![Rendered by QuickLaTeX.com \[2\textcolor{red}{x}+4\textcolor{blue}{y}+3\textcolor{olive}{a}+5\textcolor{red}{x}+2\textcolor{blue}{y}+ 7\textcolor{olive}{a}=2\textcolor{red}{x}+5\textcolor{red}{x}+4\textcolor{blue}{y}+2\textcolor{blue}{y}+3\textcolor{olive}{a}+7\textcolor{olive}{a}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6c2c571557da75d384a74d4ad413629b_l3.png)
Dadurch kannst du deine Variablen einfacher zusammenfassen:
![Rendered by QuickLaTeX.com \[2\textcolor{red}{x}+5\textcolor{red}{x}+4\textcolor{blue}{y}+2\textcolor{blue}{y}+3\textcolor{olive}{a}+7\textcolor{olive}{a}=7\textcolor{red}{x}+6\textcolor{blue}{y}+10\textcolor{olive}{a}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-873f178e52e6403d71c14fb9059220fd_l3.png)
Du musst hier aber vorsichtig sein: Beim Teilen und Subtrahieren darfst du die Reihenfolge nicht verändern:
![Rendered by QuickLaTeX.com \[-2=2-4\neq4-2=2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-08f42d447f5bfb11052e861fd3b5864f_l3.png)
![Rendered by QuickLaTeX.com \[0,5=2\div4\neq4\div2=2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-360cbc83406e96aed52cb27d3b5c2f61_l3.png)
Außerdem darfst du auch beliebig viele Klammern setzen, wenn du eine Summe oder ein Produkt in deinem Term stehen hast. Das liegt am Assoziativgesetz .
![Rendered by QuickLaTeX.com \[5+8+9=5+\left(8+9\right)=\left(5+8\right)+9\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-06bba76c6073d8ef6b81348f7e5353fc_l3.png)
![Rendered by QuickLaTeX.com \[5\cdot8\cdot9=5\cdot\left(8\cdot9\right)=\left(5\cdot8\right)\cdot9\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-294825de3ec0f299cf8bdd929631dba0_l3.png)
Wieder darfst du das nicht machen, wenn ein Minus oder ein Geteilt-Zeichen in deinem Term steht. Das würde dann deinen Wert verändern:
![Rendered by QuickLaTeX.com \[5-6+3\neq5-\left(6+3\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a3f76c764f4ff73ed7ecdee1ded59f8b_l3.png)
![Rendered by QuickLaTeX.com \[5+4\div2\neq\left(5+4\right)\div2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-98abc74228f9d64ac94c6e7be7168bf3_l3.png)
Null addieren
Eine Null addieren ist eine weitere algebraische Umformung. Du fügst deinem Term etwas hinzu und ziehst das Gleiche sofort wieder ab, sodass du den Gesamtwert nicht änderst. Schau dir dafür erst wieder ein einfaches Zahlenbeispiel an:
![Rendered by QuickLaTeX.com \[5=5+0=5+\underbrace{\textcolor{orange}{8}-\textcolor{orange}{8}}_{=0}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a35da9d4dad2c198b6635d45131f3478_l3.png)
Wenn dein Term Variablen enthält, darfst du auch eine Null addieren, da der Wert des Terms nicht verändert wird.
![Rendered by QuickLaTeX.com \[x^2+8x+4=x^2+8x+4+\underbrace{\textcolor{orange}{12}-\textcolor{orange}{12}}_{=0}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d8271e257609fd97aab280b19481adbf_l3.png)
Das hilft dir vor allem, wenn du eine quadratische Ergänzung machen musst. Dadurch kannst du deinen Term noch besser zusammenfassen und ihn in eine einfachere Form bringen:
![Rendered by QuickLaTeX.com \[x^2+2x+3=x^2+2x+\underbrace{3-\textcolor{orange}{2}}_{=\textcolor{olive}{1}}+\textcolor{orange}{2}=x^2+2x+\textcolor{olive}{1}+2=\left(x+1\right)^2+2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5293931776ac40dfd3ed3540c4926bcf_l3.png)
Binomische Formel
Jetzt hast du gelernt, Terme zu vereinfachen. Das brauchst du auf jeden Fall, wenn du mit binomischen Formeln rechnen musst. Schau dir doch direkt unser Video dazu an!