Video anzeigen

Hier geht's zum Video „Potenzgesetze“

Wurzel umschreiben

Du willst wissen, wie du eine Wurzel umschreiben kannst und was die Potenz damit zu tun hat? Dann ist dieser Artikel und unser Video genau das Richtige für dich!

Inhaltsübersicht

Wurzel umschreiben einfach erklärt

Beim Wurzel umschreiben wandelst du eine Wurzel in eine Potenz um. Die Hochzahl der Potenz ist dann ein Bruch:

$\mbox{\huge$\sqrt[\textcolor{blue}{3}]{5^\textcolor{red}{2}} = 5^{\frac{\textcolor{red}{2}}{\textcolor{blue}{3}}}$}$

Unten im Bruch (Nenner) steht der Wurzelexponent (hier: 3) und oben (Zähler) die Hochzahl unter der Wurzel (hier 2).

Zwei wichtige Spezialfälle solltest du dir merken, wenn du die Wurzel als Potenz schreiben willst:

Manchmal hat die Zahl unter der Wurzel (Radikand) keine Hochzahl. Dann ist der Zähler des Bruchs (oben) immer 1:

$\mbox{\huge$\sqrt[\textcolor{blue}{3}]{5} = 5^{\frac{\textcolor{red}{1}}{\textcolor{blue}{3}}}$}$

Manchmal siehst du keinen Wurzelexponenten. Dann ist er automatisch 2 und damit auch der Nenner des Bruchs (unten):

$\mbox{\huge$\sqrt{5^{\textcolor{red}{3}}} = 5^{\frac{\textcolor{red}{3}}{\textcolor{blue}{2}}}$}$

Wenn du die Wurzel als Potenz umschreibst, kannst du oft leichter damit rechnen .

Wurzel umschreiben Beispiele

Schau dir gleich ein paar Beispiele zum Umschreiben von Wurzeln an.

Beispiel 1: Wurzeln ohne Wurzelexponent

a) $\sqrt{2} = 2^{\frac{1}{\textcolor{blue}{2}}}$

b) $\sqrt{2^{\textcolor{red}{7}}} = 2^{\frac{\textcolor{red}{7}}{\textcolor{blue}{2}}}$

c) $\sqrt{15^{\textcolor{red}{2}}} = 15^{\frac{\textcolor{red}{2}}{\textcolor{blue}{2}}} = 15^1 = 15$

Beispiel 2: Wurzel ohne Hochzahl in der Wurzel

a) $\sqrt[\textcolor{blue}{4}]{2} = 2^{\frac{1}{\textcolor{blue}{4}}}$

b) $\sqrt[\textcolor{blue}{5}]{7} = 7^{\frac{1}{\textcolor{blue}{5}}}$

c) $\sqrt[\textcolor{blue}{3}]{21} = 21^{\frac{1}{\textcolor{blue}{3}}}$

Beispiel 3: Andere Wurzeln umformen. Denke dabei daran, dass du den Bruch in der Hochzahl ganz normal kürzen kannst.

a) $\sqrt[\textcolor{blue}{4}]{2^{\textcolor{red}{3}}} = 2^{\frac{\textcolor{red}{3}}{\textcolor{blue}{4}}}$

b) $\sqrt[\textcolor{blue}{3}]{7^{\textcolor{red}{6}}} = 7^{\frac{\textcolor{red}{6}}{\textcolor{blue}{3}}} = 7^2$

c) $\sqrt[\textcolor{blue}{4}]{2^{\textcolor{red}{2}}} = 2^{\frac{\textcolor{red}{2}}{\textcolor{blue}{4}}} = 2^{\frac{1}{2}}$

Wurzeln in Brüchen: negativer Exponent

Manchmal findest du auch eine Wurzel selbst im Nenner eines Bruchs, wie zum Beispiel bei

$\frac{1}{\sqrt[3]{5}} \qquad \text{und} \qquad \frac{2}{\sqrt{5^7}}$

Dann kannst du in zwei einfachen Schritten die Wurzel als Bruch in der Hochzahl (Exponent) schreiben. Schau dir das am Beispiel $\frac{1}{\sqrt[3]{5}}$ an:

Schritt 1: Wurzel x umschreiben: Schau dir nur die Wurzel an und schreibe sie so um, wie du es kennst.
$\sqrt[\textcolor{blue}{3}]{5} = 5^{\frac{1}{\textcolor{blue}{3}}}$

Schritt 2: Schreibe ein Minus vor dem Bruch in der Hochzahl ( $\frac{1}{\textcolor{blue}{3}}}$ ). Dann bist du fertig mit Umformen\[\frac{1}{\sqrt[\textcolor{blue}{3}]{5}} = 5^{-\frac{1}{\textcolor{blue}{3}}}\]

Achtung! Wenn im Zähler (oben) nicht nur 1 steht, musst du den Zähler zuerst vor den Bruch schreiben. Beispiel:

$\frac{\textcolor{teal}{2}}{\sqrt{5^7}}$

Schritt 1: Schreibe den Zähler mit mal vor den Bruch:
$\textcolor{teal}{2} \cdot \frac{1}{\sqrt{5^7}}$

Schritt 2: Wurzel x umschreiben:
$\sqrt{5^7}} = 5^{\frac{7}{2}}$

Schritt 3: Schreibe ein Minus vor dem Bruch in der Hochzahl ( $\frac{7}{2}}$ ).
$\textcolor{teal}{2} \cdot \frac{1}{\sqrt{5^7}} = \textcolor{teal}{2} \cdot 5^{-\frac{7}{2}}$

Wurzel umformen: Wurzelgesetze

Wurzel x umzuschreiben hilft dir oft beim Rechnen mit Wurzeln . Denn anstatt mit Wurzelgesetzen kannst du dann mit den ganz normalen Potenzgesetzen rechnen. Das hilft dir zum Beispiel, wenn du Wurzeln mit unterschiedlichen Wurzelexponenten multiplizieren möchtest. Denn beim Multiplizieren von Potenzen zählst du nur die Hochzahlen zusammen:

$\sqrt[\textcolor{red}{6}]{5} \cdot \sqrt[\textcolor{blue}{3}]{5} = 5^{\frac{1}{\textcolor{red}{6}}} \cdot 5^{\frac{1}{\textcolor{blue}{3}}} = 5^{\frac{1}{\textcolor{red}{6}} + \frac{1}{\textcolor{blue}{3}}} = 5^{\frac{1}{2}} = \sqrt{5}$

Auch wenn du Wurzeln mit einer Hochzahl hast, verwendest du am besten Potenzgesetze. Die beiden Hochzahlen nimmst du dann mal:

$(\sqrt[\textcolor{red}{3}]{5})^{\textcolor{blue}{6}} = (5^{\frac{1}{\textcolor{red}{3}}})^{\textcolor{blue}{6}} = 5^{\frac{1}{\textcolor{red}{3}}\cdot \textcolor{blue}{6}} = 5^2$

Hier siehst du weitere Wurzelgesetze und die entsprechenden Potenzgesetze auf einen Blick. Du kannst dich entscheiden, womit du lieber rechnen willst:

Wurzelgesetze

Potenzgesetze

$\sqrt[n]{\textcolor{red}{a}} \cdot \sqrt[n]{\textcolor{blue}{b}} = \sqrt[n]{\textcolor{red}{a}\cdot \textcolor{blue}{b}}}$

$\sqrt{\textcolor{red}{2}} \cdot \sqrt{\textcolor{blue}{5}} = \sqrt{\textcolor{red}{2}\cdot \textcolor{blue}{5}}} = \sqrt{10}$

$\textcolor{red}{a}^{\frac{1}{n}} \cdot \textcolor{blue}{b}^{\frac{1}{n}} = (\textcolor{red}{a} \cdot \textcolor{blue}{b})^{\frac{1}{n}}$

$\textcolor{red}{2}^{\frac{1}{2}} \cdot \textcolor{blue}{5}^{\frac{1}{2}} = (\textcolor{red}{2} \cdot \textcolor{blue}{5})^{\frac{1}{2}} = 10^{\frac{1}{2}}$

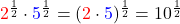
$\frac{\sqrt[n]{\textcolor{red}{a}}}{\sqrt[n]{\textcolor{blue}{b}}} = \sqrt[n]{\frac{\textcolor{red}{a}}{\textcolor{blue}{b}}}$

$\frac{\sqrt{\textcolor{red}{10}}}{\sqrt{\textcolor{blue}{5}}} = \sqrt{\frac{\textcolor{red}{10}}{\textcolor{blue}{5}}} = \sqrt{2}$

$\textcolor{red}{a}^{\frac{1}{n}} : \textcolor{blue}{b}^{\frac{1}{n}} = (\textcolor{red}{a} : \textcolor{blue}{b})^{\frac{1}{n}}$

$\textcolor{red}{10}^{\frac{1}{2}} : \textcolor{blue}{5}^{\frac{1}{2}} = (\textcolor{red}{10} : \textcolor{blue}{5})^{\frac{1}{2}} = 2^{\frac{1}{2}}$

$\sqrt[\textcolor{red}{m}]{\sqrt[\textcolor{blue}{n}]{x}} = \sqrt[\textcolor{red}{m} \cdot \textcolor{blue}{n}]{x}$

$\sqrt[\textcolor{red}{3}]{\sqrt[\textcolor{blue}{5}]{x}} = \sqrt[\textcolor{red}{3} \cdot \textcolor{blue}{5}]{x}$

$(x^{\frac{1}{\textcolor{red}{m}}}})^{\frac{1}{\textcolor{blue}{n}}} = x^{\frac{1}{\textcolor{red}{m}} \cdot \frac{1}{\textcolor{blue}{n}}}}$

$(x^{\frac{1}{\textcolor{red}{3}}}})^{\frac{1}{\textcolor{blue}{5}}} = x^{\frac{1}{\textcolor{red}{3}} \cdot \frac{1}{\textcolor{blue}{5}}}} = x^{\frac{1}{15}}$

Es gibt aber noch mehr Potenzgesetze! Wenn du sie kennenlernen willst, dann schau dir unser Video dazu an. Viel Spaß!

Potenzgesetze — zum Video: Potenzgesetze

Beliebte Inhalte aus dem Bereich Mathematische Grundlagen

Kubikwurzel

Dauer: 02:31

Wurzeln addieren und subtrahieren

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .