Video

Quiz

Hier geht's zum Video „Umfang Rechteck“

Hier geht's zum Video „Kreisberechnung“

Punktsymmetrie

Wichtige Inhalte in diesem Video

Was bedeutet punktsymmetrisch?

Punktsymmetrische Figuren

Punktsymmetrische Funktionen

In diesem Beitrag erklären wir dir, was du unter der Punktsymmetrie verstehst und wie du Punktsymmetrie bei Figuren und Funktionen erkennen kannst. In unserem Video erklären wir dir das Thema anschaulich. Schau es dir an!

Inhaltsübersicht

Was bedeutet punktsymmetrisch?

im Videozur Stelle im Video springen

Eine Figur ist punktsymmetrisch, wenn du sie um 180° drehen kannst, ohne dabei ihr Aussehen zu verändern. Wenn du eine Figur um 180° drehst, stellst du sie einfach auf den Kopf.

Rechteck, Punkt, Seite, Drehen, Punktsymmetrie — punktsymmetrisches Rechteck

Dabei drehst du die Figur um ein Spiegelzentrum oder Spiegelpunkt. Daher kommt auch der Name Punktsymmetrie.

Du kannst auch überprüfen, ob eine Funktion f punktsymmetrisch zum Ursprung ist. Ist das der Fall, dann gilt für die Funktion f

$\textbf{f(\textcolor{blue}{-x}) = \textcolor{red}{-}f(x)}$ .

Schauen wir uns nun konkrete Beispiele zur Punktsymmetrie an.

Punktsymmetrische Figuren

im Videozur Stelle im Video springen

Starten wir mit einem Quadrat.

Quadrat, Symmetrie — Quadrat mit Symmetriepunkt

Wenn du ein Quadrat um 180° drehst, stellst du es auf den Kopf. Das ändert aber nichts an seinem Aussehen. Es ist also deckungsgleich und punktsymmetrisch um das Symmetriezentrum.

Rechteck

Ein Rechteck ist ebenfalls punktsymmetrisch.

Parallelogramm, Rechteck — Parallelogramm

Ein Parallelogramm ist eine Art „verschobenes“ Rechteck und weist auch Punktsymmetrie auf.

Kreis, Punktsymmetrie — Kreis

Ein Kreis ist ebenso punktsymetrisch zu seinem Mittelpunkt.

Punktsymmetrische Funktionen

im Videozur Stelle im Video springen

Auch bei Funktionen gibt es Punktsymmetrie und dafür hast du eine Punktsymmetrie Formel. Eine Funktion ist punktsymmetrisch zum Ursprung , wenn gilt

$\textbf{f(\textcolor{blue}{-x}) = \textcolor{red}{-}f(x)}$ .

Beispiel 1

im Videozur Stelle im Video springen

Nehmen wir mal an, du sollst überprüfen, ob die Funktion f(x) = x^3 punktsymmetrisch zum Ursprung ist. Wie gehst du vor?

1. f(-x) berechnen: Ersetze in der Funktion x^3 alle x durch -x. Denk daran: Minus mal Minus ergibt Plus!

$f(\textcolor{blue}{-x}) = (\textcolor{blue}{-x})^3 = (\textcolor{blue}{-x}) \cdot (\textcolor{blue}{-x}) \cdot (\textcolor{blue}{-x})= x^2 \cdot (\textcolor{blue}{-x}) =-x^3$

2. –f(x) berechnen: Du bekommst –f(x), indem du einfach ein Minus vor x^3 schreibst.

$\textcolor{red}{-}f(x) = -x^3$

3. Symmetrie bestimmen: Vergleiche die beiden Funktionen.

$f(\textcolor{blue}{-x}) = -x^3$

$\textcolor{red}{-}f(x)=-x^3$

Da die Funktionen gleich sind, ist die Punktsymmetrie Formel erfüllt, 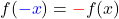$f(\textcolor{blue}{-x}) = \textcolor{red}{-}f(x)$ . Die Funktion f(x)=x^3 ist damit punktsymmetrisch.

Symmetriezentrum, Funktion, Punktsymmetrie, Graph — Funktion f(x) mit Punktsymmetrie

Beispiel 2

im Videozur Stelle im Video springen

Schauen wir uns als nächstes an, wie du bei der Funktion f(x) = 2x^3 + x^2 - 9x prüfst, ob sie punktsymmetrisch zum Ursprung ist.

1. f(-x) berechnen: Setze wieder -x für x in die Funktion ein.

$f(\textcolor{blue}{-x}) = 2 \cdot (\textcolor{blue}{-x})^3 + (\textcolor{blue}{-x})^2 - 9\cdot(\textcolor{blue}{-x})= \textcolor{orange}{-2x^3 + x^2 + 9x}$

2. –f(x) berechnen: Du kannst –f(x) berechnen, indem du ein Minus vor die Funktion schreibst. Achte darauf, dass du eine Klammer um die Funktion setzt und dann die Minus-Klammer auflöst.

$\textcolor{red}{-}f(x) = \textcolor{red}{-}(2x^3 + x^2 - 9x) = \textcolor{violet}{-2x^3 - x^2 + 9x}$

3. Symmetrie bestimmen: Und wieder schaust du, ob beide Gleichungen dasselbe Ergebnis haben.

$f(\textcolor{blue}{-x}) = \textcolor{orange}{-2x^3 + x^2 + 9x}\ \texbf{\neq} \ \textcolor{violet}{-2x^3 - x^2 + 9x} = \textcolor{red}{-}f(x)$

Diesmal gilt die Punktsymmetrie Formel nicht, woraus du schließen kannst, dass die Funktion f(x) = 2x^3 + x^2 - 9x nicht punktsymmetrisch zum Ursprung ist.

Funktion, Punktsymmetrie, Graph, Symmetriepunkt — Funktion f(x) ohne Punktsymmetrie

Quiz zum Thema Punktsymmetrie

Achsensymmetrie

Neben der Punktsymmetrie gibt es auch noch die Achsensymmetrie, bei der du entlang einer bestimmten Achse spiegelst. Für deine nächste Prüfung solltest du sie kennen. Schau dir jetzt direkt unser Video dazu an!

Zum Video: Achsensymmetrie, Punktsymmetrie — Zum Video: Achsensymmetrie

zur Videoseite: Punktsymmetrie

Beliebte Inhalte aus dem Bereich Geometrie

Achsensymmetrie

Punktspiegelung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .