Geometrie
Die Geometrie ist ein wichtiger Teil der Mathematik. Welche Themenbereiche dazugehören und was für Grundlagen du kennen solltest, zeigen wir dir hier und im Video !
Inhaltsübersicht
Was ist Geometrie? — einfach erklärt
Geometrie ist ein Teilgebiet der Mathematik. Sie beschäftigt sich mit Formen, Größen und der Anordnung von Figuren im Raum. In der Schule lernst du die sogenannte Elementargeometrie (euklidische Geometrie). Dabei beschäftigst du dich mit einfachen Formen wie Punkten, Geraden und Ebenen. Du lernst, wie du Abstände misst, Winkel berechnest und die Position von Figuren im Raum bestimmst.
Übrigens: Der Begriff kommt vom altgriechischen Wort „geometria“ und bedeutet so viel wie „Erdmessung“ oder „Landmessung“.
Geometrie — Grundbegriffe
In der Geometrie sind einige Grundbegriffe besonders wichtig. Sie bilden nämlich die Basis für alle anderen Bereiche der Geometrie. Dazu gehören:
-
Punkt: Ein Punkt ist der einfachste geometrische Grundbegriff. Er hat keine Länge, Breite oder Höhe. Einen Punkt markierst du oft durch einen kleinen Kreis oder ein Kreuz und bezeichnest ihn mit einem Großbuchstaben, zum Beispiel Punkt A.
-
Gerade: Eine Gerade ist eine unendlich lange Linie, die in beide Richtungen ohne Ende verläuft. Sie hat keine Kurven und wird mit einem Kleinbuchstaben gekennzeichnet, zum Beispiel Gerade g.
-
Strecke: Eine Strecke
ist eine Gerade, die durch zwei Punkte begrenzt wird. Diese beiden Punkte werden als Endpunkte der Strecke bezeichnet. Zum Beispiel ist die Strecke AB die Verbindung zwischen Punkt A und Punkt B.
- Winkel: Winkel entstehen durch zwei sich schneidende Geraden. Die beiden Geraden schließen dabei den Winkel ein. Winkel gibst du in Grad an und kennzeichnest sie mit griechischen Buchstaben wie α (Alpha).
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Geometrische Formen und Figuren
Auf Basis der Grundlagen folgen die geometrischen Formen und Figuren. Dazu gehören zweidimensionale Figuren wie Dreiecke, Vierecke und Kreise. Aber auch die Eigenschaften der Figuren sind Teil des Themenbereichs. Wie zum Beispiel der Flächeninhalt und der Umfang.
Zu den wichtigsten Figuren gehören:
- Dreiecke
- Vierecke — Dazu zählen Rechtecke, Quadrate, Parallelogramme, Trapeze, Rauten und andere Vielecke.
- Kreise
Alle wichtigen Formeln zur Berechnung der Fläche und des Umfangs der verschiedenen Figuren findest du hier:
| Fläche Dreieck:
A =  • g • h • g • h |
Umfang Dreieck:
U = a + b + c |
| Fläche Rechteck:
A = a • b |
Umfang Rechteck:
U = 2 • (a + b) |
| Fläche Quadrat:
A = a2 |
Umfang Quadrat:
U = 4 • a |
| Fläche Parallelogramm:
A = a • ha |
Umfang Parallelogramm: U = 2 • (a + b) |
| Fläche Trapez:
A =  • (a + c) • h • (a + c) • h |
Umfang Trapez:
U = a + b + c + d |
| Fläche Kreis:
A = π • r2 |
Umfang Kreis:
U = 2 • π • r |
Konstruktion von geometrischen Formen
Nachdem du nun die zweidimensionalen Flächen kennengelernt hast, schauen wir uns an, wie du diese Formen selbst zeichnen kannst. Geometrische Konstruktion bedeutet, dass du mithilfe von Lineal und Zirkel präzise Zeichnungen erstellst. Hier sind die wichtigsten Messungen und Methoden, die du kennen solltest:
- Strecken abtragen
- Winkel messen
- Parallele Geraden zeichnen
- Senkrechte zeichnen
- Mittelsenkrechte konstruieren
- Winkelhalbierende zeichnen
Neben den grundlegenden Konstruktionsmethoden gibt es auch wichtige Konzepte wie Kongruenz, Ähnlichkeit und Symmetrie, die dir helfen, geometrische Formen besser zu verstehen und zu zeichnen:
- Kongruenz: Zwei geometrische Figuren sind kongruent, wenn sie deckungsgleich sind, also dieselbe Form und Größe haben.
- Ähnlichkeit: Haben zwei Figuren nur dieselbe Form, aber unterschiedliche Größen, sind sie sich ähnlich.
- Symmetrie: Eine Figur ist symmetrisch, wenn sie durch eine Linie in zwei gleiche Hälften geteilt werden kann. Es gibt verschiedene Arten von Symmetrie, wie Achsensymmetrie und Punktsymmetrie.
Geometrische Körper (Raumgeometrie)
Während die geometrischen Figuren sich mit zweidimensionalen Formen beschäftigten, geht es bei den geometrischen Körpern um dreidimensionale Objekte. Du sprichst daher auch von der Raumgeometrie. Viele davon kennst du bestimmt schon: Kugeln, Würfel oder Kegel. Diese Objekte haben Länge, Breite und Höhe. Alle geometrischen Körper besitzen außerdem Kanten, Ecken oder Spitzen — außer die Kugel.
Zu den wichtigsten räumlichen Figuren gehören:
Außerdem lernst du, wie du das Volumen und den Oberflächeninhalt von Körpern berechnest. Hier siehst du die wichtigsten Formeln dazu:
| Volumen Quader:
V = a • b • c |
Oberfläche Quader: O = 2 • a • b + 2 • a • c + 2 • b • c |
| Volumen Würfel:
V = a3 |
Oberfläche Würfel: O = 6 • a2 |
| Volumen Pyramide:
V = 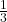 • G • h • G • h |
Oberfläche Pyramide:
O = G + M |
| Volumen Kegel:
V = 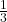 • π • r2 • h • π • r2 • h |
Oberfläche Kegel:
O = π • r2 + π • r • s |
| Volumen Zylinder:
V = r2 • π • h |
Oberfläche Zylinder:
O = 2 • π • r • (r + h) |
| Volumen Kugel:
V =  • π • r3 • π • r3 |
Oberfläche Kugel:
O = 4 • π • r2 |
Übrigens: Auch geometrische Körper kannst du zeichnen. Dafür nutzt du meist das Schrägbild oder Körpernetze.
Geometrie — Trigonometrie
Die Trigonometrie ist ein spezieller Bereich der Geometrie. Hier dreht sich alles um das Dreieck und seine Eigenschaften. Zum einen gibt es verschiedene Arten von Dreiecken, wie das gleichseitige Dreieck und das gleichschenklige Dreieck.
Zum anderen lernst du verschiedene Beziehungen kennen, die dir helfen, Dreiecke zu berechnen und zu konstruieren. Dazu gehören:
Eine besondere Rolle nimmt das rechtwinklige Dreieck ein. Denn dessen Seiten haben bestimmte Namen. So nennst du die längste Seite Hypotenuse. Sie liegt immer gegenüber von dem 90°-Winkel. Die anderen beiden Seiten sind die Katheten. Je nachdem welchen Winkel (α oder β) du betrachtest, sprichst du auch von Ankathete und Gegenkathete.
In dem Zusammenhang lernst du auch den Satz des Pythagoras (a2 + b2 = c2) und Sinus, Cosinus, Tangens kennen.
Analytische Geometrie
Die analytische Geometrie verbindet Algebra und Geometrie. Hier beschreibst du geometrische Objekte wie Punkte, Geraden und Ebenen mithilfe von Koordinaten und Gleichungen. Dafür nutzt du zwei- und dreidimensionale Koordinatensysteme, um zum Beispiel die Lage von Punkten zu bestimmen.
Ein wichtiger Teil der analytischen Geometrie sind Vektoren. Du bezeichnest den Bereich daher auch als Vektorgeometrie. Vektoren sind Strecken, die sowohl eine Richtung als auch eine Länge haben. Du verwendest sie, um die Lage von Punkten im Raum zu beschreiben oder um die Bewegung von einem Punkt zu einem anderen darzustellen.
Weitere wichtige Themen der analytischen Geometrie sind:
- Geraden und Ebenen als Gleichungen
- Lagebeziehungen von Geraden
- Abstandsberechnungen — Dazu gehören der Abstand zweier Punkte, zwischen zwei Geraden oder zwischen einem Punkt und einer Ebene.
Geometrie — häufigste Fragen
(ausklappen)
Geometrie — häufigste Fragen
(ausklappen)-
Was ist Geometrie in Mathe kurz erklärt?Geometrie ist ein Teilgebiet der Mathematik, das Formen, Größen und Lagebeziehungen von Figuren beschreibt. Du arbeitest mit Grundbegriffen wie Punkt, Gerade, Strecke, Winkel und Ebene. Typische Aufgaben sind Längen und Winkel berechnen sowie Figuren im Raum einordnen.
-
Was ist der Unterschied zwischen einem Punkt, einer Geraden und einer Strecke?Ein Punkt ist nur eine Position ohne Ausdehnung, also ohne Länge, Breite oder Höhe. Eine Gerade ist eine gerade Linie, die in beide Richtungen unendlich weiterläuft. Eine Strecke ist ein begrenzter Teil einer Geraden und hat genau zwei Endpunkte.
-
Wie berechne ich den Flächeninhalt von einem Dreieck?Den Flächeninhalt eines Dreiecks berechnest du mit
 , wobei
, wobei  die Grundseite und
die Grundseite und  die zugehörige senkrechte Höhe ist. Konkret bedeutet das: Bei
die zugehörige senkrechte Höhe ist. Konkret bedeutet das: Bei  und
und  gilt
gilt  .
.
-
Wie zeichne ich eine Mittelsenkrechte mit Lineal und Zirkel?Eine Mittelsenkrechte ist die Gerade, die eine Strecke in der Mitte teilt und senkrecht auf ihr steht. Konkret bedeutet das: Zeichne Strecke
 , stelle den Zirkelradius größer als die halbe Strecke ein, schlage um
, stelle den Zirkelradius größer als die halbe Strecke ein, schlage um  und um
und um  Kreisbögen, verbinde die zwei Schnittpunkte der Bögen mit dem Lineal.
Kreisbögen, verbinde die zwei Schnittpunkte der Bögen mit dem Lineal.
-
Was ist der Unterschied zwischen Kongruenz und Ähnlichkeit?Kongruenz bedeutet, dass zwei Figuren deckungsgleich sind, also gleiche Form und gleiche Größe haben. Ähnlichkeit bedeutet, dass die Form gleich ist, die Größe aber abweichen darf. Dann sind entsprechende Winkel gleich und entsprechende Seitenlängen stehen im gleichen Verhältnis (Skalierungsfaktor).
Funktionstypen
Neben der Geometrie spielt auch der Bereich der Analysis eine große Rolle im Mathematikunterricht. Ein Teil davon sind die verschiedenen Funktionstypen. In unserem Video erklären wir dir, welche es gibt und was ihre Eigenschaften sind.





